Effektiver Zinssatz?

Hallo zusammen,
weiß jemand von euch, wie ich den Term nach dem effektiven Zinssatz auflösen kann?
Ich könnte den Term im Nenner solange multiplizieren, bis der Nenner verschwindet, oder? Dann brauche ich aber ewig, bis ich auf ein Ergebnis komme.
Sonst könnte ich das ganze noch mit der internen Zinsfuß Regel machen, oder? Also dass ich einfach zwei Versuchszinssätze nehme und dann eben diese Methode anwende.
Aber würde es noch eine andere, einfachere Methode geben, um auf den effektiven Zinssatz zu kommen?
3 Antworten
Multiplizieren Sie beide Seiten der Gleichung mit (1+i), anschließend ausmultiplizieren und die Gleichung auf die Form "ax³+bx²+cx+d=0" bringen. Damit wird die Ermittlung des effektives Zinssatzes zu einem Nullstellenproblem. Eine analytische Lösung kann dann mit den Cardanischen Formeln ermittelt werden. Der von mir approximativ ermittelte Wert für i beträgt 0,045 (siehe Abbildung; der Graph schneidet die x-Achse bei (i,0)).

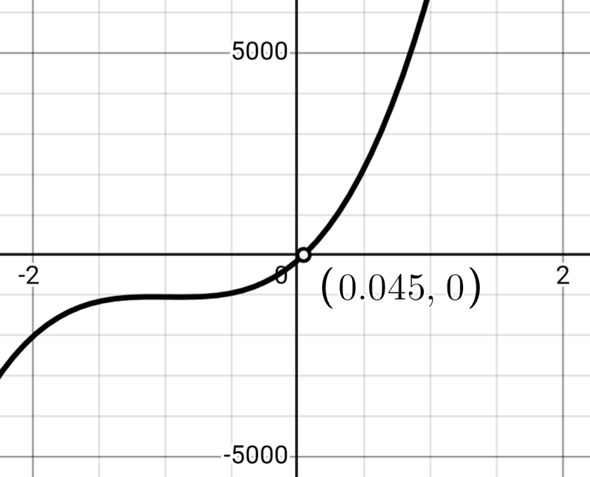
Wenn ich mich recht entsinne, haben Sie mich das schon einmal gefragt. Ich schreibe meine Antworten nach wie vor selbst.
ja , mal (1+i)³ wäre ein Ansatz , der aber wegen der linken Seite
986unleserlich * (1+i)³ auf jeden Fall zu einer Glg dritten Grades führen würde , die man normal nicht lösen kann
.
f(x) = -986 + 40/(1+x) + 40/(1+x)² + 1040/(1+x)³
als Fkt wählen und die Nullstelle suchen
Durch Probieren ( ich wählte 0.04 und 0.05 für i ) siehe hier komme ich mit 0.045 dem wahren i schon sehr nahe
- (1+i)^3
Ja. du multiplizierst mit (1+i)^3 damit du das i aus dem Nenner bekommst. Danach kannst du einfach nach i auflösen.
chatGPT ?