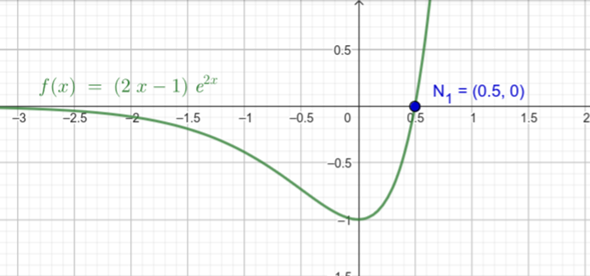
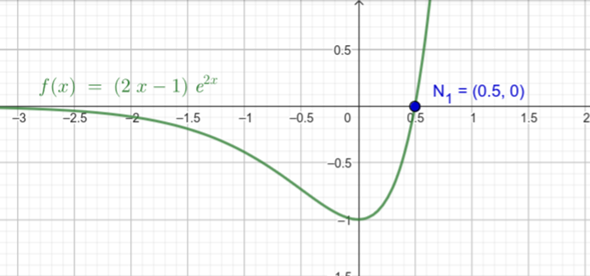
0=(2x-1)e^2x mit ln(...) umformen; auf rechter Seite dann ln((2x-1)e^2x)?

Hallo,

da es oben im Titel eher kompliziert aussieht hier nochmal "schöner"

Ich habe den Term (um die Nullstellen zu berechnen): $0=\left(2x-1\right)e^{2x}$ Um das e wegzubekommen möchte ich ln(...) anwenden (wobei ich weiß, dass ln(0) undefiniert ist). Nur ist meine Frage dann, ob es auf der rechten Seite ... $\ln\left(\left(2x-1\right)e^{2x}\right)$ oder nur ...

$\ln\left(e^{2x}\right)$

Ich denke die erste Version wäre richtig. Sollte das der Fall sein, wie würde ich sowas auflösen?

Aber die Nullstelle bekomme sogar ich noch hin: x = 0,5 weil siehe Klammer.
Da e^n =/= 0 ist, müsste ich das theoretisch nicht beachten (... oder?).

Ich weiß, dumme Frage aber ich bin echt grottenschlecht in Mathe allgemein und noch schlechter in der Analysis.

Answer 1

[tunik123]

x = 0,5 ist richtig. Aber ein Logarithmus ist nicht nötig. Die e-Funktion kann niemals 0 werden, also muss 2x - 1 = 0 sein.

Answer 2

[Willy1729]

Hallo,

Du hast ein Produkt mit e hoch irgendetwas. e hoch irgendetwas wird niemals Null.

Das Produkt kann nur Null werden, wenn der andere Faktor, der ohne e, Null wird.

Das ist hier der Term 2x-1.

Es reicht also, 2x-1=0 zu lösen. Dazu brauchst Du keinen Logarithmus.

Herzliche Grüße,

Willy

Answer 3

[Aurel8317648]

Du darfst durch e^(2x) dividieren da das nie Null werden kann, und somit fällt das weg und dann ist die Gleichung ganz einfach:

0 = 2x- 1

Answer 4

[Maxi170703]

Der ln(0) ist nicht definiert, denn e^x ist niemals 0, für kein x

Answer 5

[evtldocha]

Satz vom Nullprodukt und fertig:

$x=\frac{1}{2}$