Analytische geometrie kugeln?
Wie löse ich die aufgabe b?

4 Antworten
Aufgabe b)
Die Gerade g2 durch BM lautet:
g2(r) = (5,3,3) + r*(2,-4,-1)
Die Kugelgleichung lautet:
(x-7)² + (y+1)² + (z-2=)² = 21
Geradengleichung in die Kugelgleichung einsetzen:
((5+2r)-7)² + ((3-4r)+1)² + ((3-r)-2)² = 21
Lösung r1 = 0, r2 = 2
g2(0) = B (wie zu erwarten)
g2(2) = (9,-5,1) (Schnittpunkt)
Sorry, ich habe eine Koordinate vertauscht. Habe meine Antwort korrigiert.
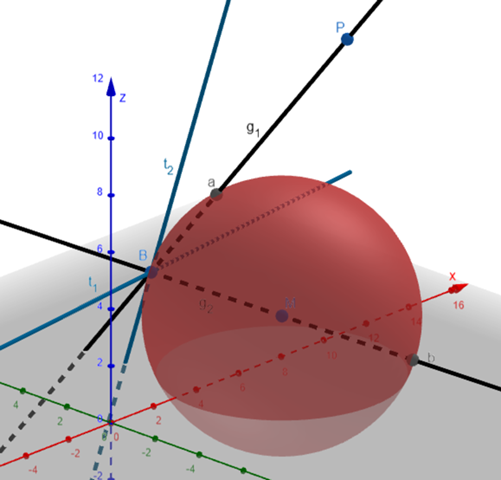
Ich hab den ganzen Spaß mal in Geogebra nachgebaut:

Bei Aufgabe B ist der gesuchte Punkt einfach genau auf der gegenüberliegenden Seite der Kugel. Das löst du, indem du den Abstand zwischen Punkt B und dem Mittelpunkt der Kugel berechnest, und dann einfach nochmal den gleichen Abstand dazuaddierst.
Abstand = M-B = (7, -1, 2) - (5, 3, 3) = (2, -4, -1)
P = M+Abstand = (7, -1, 2) + (2, -4, -1) = (9, -5, 1)
Ein Durchmesser geht immer durch den Mittelpunkt. Mit B und M kann man daher die Geradengleichung aufstellen. Das wäre dann meine Lösung:


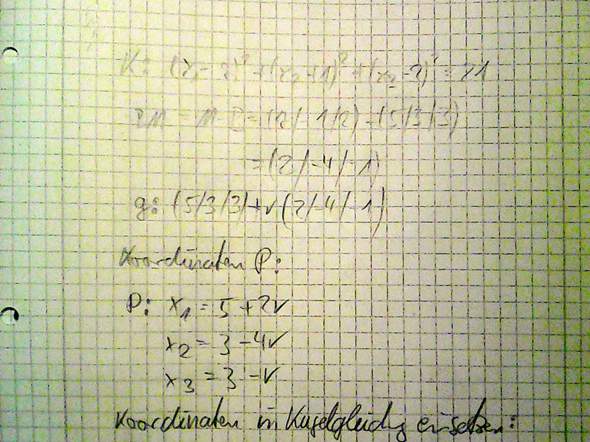

Soweit ich das verstehe ist die Schnittmenge der Kugel mit der geraden so groß, dass das teilstück der Geraden, das in der Kugel ist, so lang ist wie ein Durchmesser der Kugel.
Damit kann man entweder eine Gleichung aufstellen oder man interpretiert das direkt so, dass die Gerade durch den Mittelpunkt der Kugel geht (sonst wäre die Schnittstrecke kürzer als ein Durchmesser).
Und damit kann man dann weiterarbeiten und die Frage beantworten.
Danke. g2(r) = (8,-3,12) + r*(-1,2,-10) woher kommst du darauf