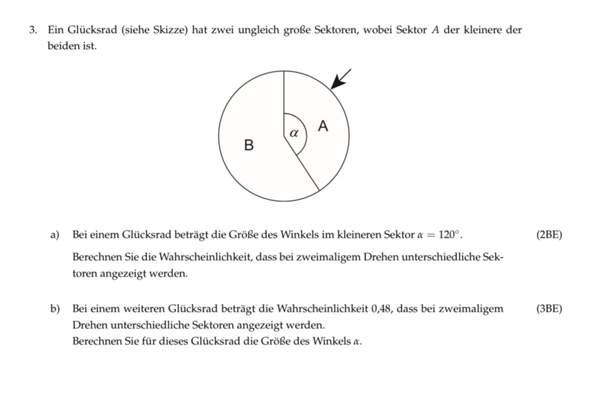
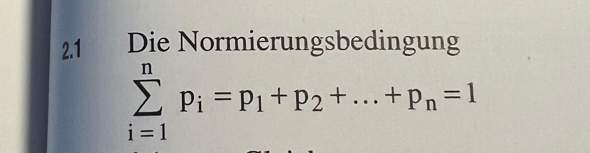Folgende Aufgabe wurde gestern im Mathe-LK Abitur in Hessen im Stochastik-Teil so oder so ähnlich gestellt:
Niclas möchte auf einer Online-Plattform ein Kennwort mit acht Zeichen erstellen.
Zur Auswahl stehen 26 Groß- und Kleinbuchstaben, 18 Sonderzeichen und 10 Zahlen, insgesamt also 80 Zeichen.
Er möchte nun ein Passwort unter folgenden Bedingungen erstellen:
- Sein Name „Niclas“ soll in richtiger Reihenfolge im Passwort enthalten sein.
- Keine der 80 Zeichen soll zweimal verwendet werden.
Damit wären Ni*cl8as, !Nicla?s oder Nicla5ns mögliche Passwörter.
Wie viele Möglichkeiten für diese Art von Passwort gibt es?
Mein Gedanke war, dass es doch 30 Möglichkeiten gibt, zwei weitere Zeichen in den sechs Buchstaben des Namens zu ergänzen (unter Berücksichtigung der Reihenfolge). Jede dieser 30 Möglichkeiten hat wiederum 74*73 Möglichkeiten, weil es für das erste hinzugefügte Zeichen noch 74, und für das zweite hinzugefügte Zeichen noch 73 Möglichkeiten gibt.