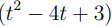Unimathe – die meistgelesenen Beiträge

Hallo!

Wenn nach Eigenvektoren v zu einem Eigenwert w einer Matrix A gefragt wird suche ich zunächst immer nach kern(A-wE), also dem Eigenraum. (E ist nxn Einheitsmatrix). Danach suche ich mir einen der Basisvektoren des Eigenraums raus und habe einen Eigenvektor.

Jetzt habe ich im Internet verschiedene Notationen gesehen... Beim aufschreiben des Eigenraums: Beispiel: Eig(w)={t*v | t aus C}. t=0 wurde NICHT ausgeschlossen. Jemand anderes wiederum hat nach einem Eigenvektor gesucht und kam durch das lösen des LGS auf t*v und hat gesagt, dass t nicht Null sein darf... Deswegen bin ich ein bisschen verwirrt... ist die Null im Eigenraum, darf aber nicht als Eigenvektor gewählt werden?

Ich stieß eben auch auf eine Aufgabe, bei welcher ich sagen sollte ob es richtig oder falsch ist, dass (0,0,0)^T aus Q^3 Eigenvektor einer gegebenen Matrix ist...

Danke und LG

Hallo!

Ich studiere Mathe und bin gerade im zweiten Semester. Das Semester neigt sich dem Ende hin und wir schreiben bad Klausuren. Wir haben im ersten Semester keine Klausuren geschrieben und schreiben nun Analysis 1+2 und Lineare Algebra 1+2. Bedeutet Stoff von zwei Semestern! Wir haben im ersten Semester einer Probeklausur in Analysis 1 geschrieben, bei der ich relativ schlecht abgeschlossen habe. Verwundert mich aber nicht, denn es hat von über 100 Leuten nur einer theoretisch bestanden und ich habe mich ehrlich gesagt nicht soo richtig gut vorbereitet. Vor etwa einem Monat haben wir eine LinA Probeklausur geschrieben die mir relativ leicht viel.

Also. In einer Woche ist Vorlesungsfreie Zeit. Bedeutet in ca. 5 bis 6 Wochen schreibe ich Analysis und dann nach weiteren 3 bis 4 Wochen Lineare Algebra.

Mein Plan:

Erst das Skript von vorne bis hinten durcharbeiten, dann vergangen Übungszettel durcharbeiten (Musterlösungen studieren und selber bearbeiten) und dann Klausuren von Vorjahren und anderen Unis bearbeiten.

Natürlich gibt es nicht die EINE Lernstrategie die für jeden am besten ist. Trotzdem würde ich gerne nach Tipps fragen! Wäre cool, wenn ihr vielleicht aus Erfahrungen berichten könnt und/oder sagen, ob ihr Teile zu meinem Plan hinzufügen oder vielleicht ändern würdet.

Danke!

LG Max Stuthmann

Guten Tag!

Sei A=(a,b] das halboffene reelle Intervall mit a<b, in welchem das a aber nicht das b enthalten ist. Jetzt frage ich mich, ob dieses Intervall als offene oder abgeschlossene Teilmenge der Reellen Zahlen eingestuft werden kann. Für abgeschlossen habe ich eine Begründung und für offen auch. Nur bei offen bin ich mir nicht ganz sicher ob das so hin haut, wie ich mir das denke.

Also. Zunächst sei Br(x) eine offene Umgebung um x mit dem Radius r>0. Dann ist eine Teilmenge V eines Metrischen Raumes X offen, wenn für alle x0 aus X gilt, dass ein r existiert, sodass Br(x0) Teilmenge von V ist. Dies ist hier ja offensichtlich nicht der Fall. Wenn ich nun b=x0 wähle, ist für jedes r>0 die Umgebung Br(b) nicht Teilmenge von A=(0,1]. Somit müsste A ja abgeschlossen sein, denn wenn sie nicht offen ist muss sie ja abgeschlossen sein. ABER: In meinem Skript steht als Definition:

1. Eine Teilmenge V von X heißt offen, wenn [...] gilt.
2. Eine Teilmenge W von X heißt abgeschlossen, wenn X\W offen ist (X\W ist das Komplement von W)

Wähle ich nun als unseren Metrischen raum das reelle Intervall B=[a-1,b] ist A Teilmenge davon. Nun folgende Argumentation:

B\A=[a-1,a] ist offensichtlich abgeschlossen. Daraus folgt laut des zweiten Teils der Definition, dass A offen ist.

Ich habe gelernt, dass die leere Menge und R selber offen und abgeschlossen zugleich sind, jedoch nicht, dass gleiches für Halboffene Intervalle gilt.

Aufklärungsbedarf! Ich würde mich über eine kurze Antwort auf die Frage im Titel und eine kurze Begründung freuen! Hinweise auf Fehler in meiner Argumentation würden ich auch begrüßen

Danke und LG

Max Stuthmann

Hey

Ist die strukturelle Induktion dasselbe wie die Vollständige? Also beginnen mit Induktionsanfang, -annahme und -schritt?

Und könnte jemanden das hier lösen oder zumindest eine davon, damit ich sehen kann, wie das ist.

Hier steht er habe zwei, aber wie? Körperautomorphismus heißt doch Selbstabbildung? Ich kann doch nur einmal auf mich selbst abbilden?

Mir macht eine Aufgabe im Mathestudium schwer zu schaffen:

Aufgabe 2.1. Sei Q[ √ 2] die folgende Teilmenge der Menge der reellen Zahlen:
Q[ √ 2] = {x + y √ 2; x, y ∈ Q}.

Zeigen Sie, dass Q[ √ 2] mit der Addition und Multiplikation reeller Zahlen ein Körper ist.

Meine Idee ist, dass mit den Körperaxiomen für Addition und Multiplikation zu beweisen, aber ich weiß einfach nicht wie...

Hoffe jemand kann mir helfen^^'

Hallo!

Hier ein Diagramm:

[(K ist Körper; V,W sind K-Vektorräume; M(f) ist Darstellungsmatrix bzgl. angegebener Basen; T sind Basistransformationsmatrizen und f ist K-Lineare Abbildung)]

Also eigentlich verstehe ich alles ganz gut rund um dieses Thema. Dennoch geht es um diese Phi´s in dem Bild...

Die Abbildungen Phi sind Isomorphismen. Diese Isomorphismen existieren hier, da vorher bedingt wurde, dass V eine Basis A=(a_1,...,a_n) und W die Basis B=(b_1,...,b_m) hat und somit V isomorph zu K^n und W isomorph zu K^m ist.

Naja meine Frage ist: Ist es nicht überflüssig über die K^n und K^m zu gehen? Ich meine könnt ihr mir ein Beispiel eines endlich dimensionalen K-Vektorraums geben, welcher nicht direkt der "Form" K^d entspricht? Ich meine so Funktion- und Folgenräume sind doch alle nicht endlich dimensional... Bedeutet es gibt doch gar keinen endlich dimensionalen K-Vektorraum, welcher NICHT einfach nur K^n ist. Wieso brauche ich dann in diesen Diagrammen diese Isomorphismen? Wieso wird V als K^n übersetzt, obwohl V=K^n?

Oder habt ihr ein Beispiel ?

Danke und LG Max!

Guten Tag:

Seien I_n mit n aus N nichtleere abgeschlossene Intervalle in R, sodass I_(n+1) teilmenge von I_n ist. Dann ist der Schnitt dieser Intervalle (für n=1 bis unendlich) nicht leer.

Okay, das mag ja sein, aber hier steht, es gilt NICHT für offene Intervalle und wir sollen uns da mal ein Beispiel überlegen. Aber wieso gilt dies denn nicht für offene Intervalle und hätte jemand da n Beispiel?

Danke und LG Max Stuthmann

Hallo,

Ich verstehe was Modulo macht. Aber ich würde gerne verstehen warum man bei großen Zahlen, die man nicht im Kopf rechnen kann , erstmal dividiert, dann die Nachkommastellen ignoriert, drittens dieses neue Ergebnis mit dem divisor multipliziert. Und letztlich dieses Ergebnis vom Dividenden abzieht. Also warum kommt man so zum Ergebnis ? Ich will es logisch verstehen, nachvollziehen und nicht einfach so anwenden.

Danke .

Könnte man es beispielsweise hier nachweisen wenn ja wie?

Kurze Frage: Was ist die Summenreihenentwicklung des Pochhammer Symbols?

In Mathworld über das Pochhammer Symbol steht als geschlossende Form eine Summenreihenentwicklung mit



wobei s(n, k) die Stirling Zahl der ersten Art ist.

Im Mathworld Artikel zur Stirling Zahl der ersten Art steht jedoch als Potenzreihentwicklung für die Stirling Zahl der ersten Art



Aber die beiden Reihentwicklungen sind doch unterschiedlich:



Eine andere verbreitete Schreibweise des Pochhammer Symbols ist



wobei Gamma(x) für die vollständige Gammafunktion von x steht.

Frage steht schon im Titel:

Gibt es eine Menge M, deren Potenzmenge eine Partition von M ist?

Bin mir nicht sicher, meine Antwort wäre: nein, da in Potenzmengen leere Mengen enthalten sind und in Partitionen nicht. (ist das richtig so)

Habe aus der vorangegangenen Schule noch einen ziemlich guten Grafikrechner mit allen möglichen Funktionen, welche ich allerdings auch einfach mit einem Computerprogramm oder online durchführen könnte.

Sind Taschenrechner überhaupt zu Matheprüfungen im Studiengang Informatik (in Bayern) zugelassen und wenn ja, welche Art - Grafikrechner (CASIO fx-7400GII) oder normaler Schultaschenrechner (CASIO fx-87DE PLUS)?

Dozent hat geschrieben, dass die Nullstellen reel sind, können ganzzahlig sein, müssen aber nicht, der Satz von Vieta lautet:

korrekt?
Darf man den allgemein anwenden oder nur, wenn die Ergebnisse ganzzahlig isnd? Hie rhat es geklappt, ich frage mich nur,w as wäre wenn es nicht ganzzahlig wäre, dürfte ich dann den Satz noch anwenden?

Ich habe eine Aufgabe gegeben, in der ich die Orthogonale Projektion von einem Punkt (1,7) zu einer Geraden berechnen soll, die durch den Ursprung und Punkt (-4,2) läuft.

An sich kein Problem, ich habe den Vektor (-2,1)^T als Ergebnis. Aber das macht doch keinen Sinn!

Der Vektor ist ja linear abhängig zu (-4,2)^T und würde also auf der gleichen gerade liegen?!?! Also auf keinen Fall orthogonal dazu stehen.
Was verstehe ich hier nicht?

(Die Lösung ist laut der Musterlösung korrekt.)

Edit:
Ich denke ich habe verstanden, dass der Vektor, den ich als Ergebnis habe offenbar nicht die Strecke von dem Punkt auf die Gerade angibt, sondern den Punkt (als Vektor), auf den die Projektion auf der Gerade treffen würde.

Binomische Formel Spezialfall wenn ich sowas habe iwe (-1-3)^2 ist das dann 1-6+9 oder 1+6+9? Normalerweise besagt die FOrm, dass es minus sein sollte? Aber in dem Falle, kommt ja 16 raus, also positiv, soimit gilt die regel, dass das mittlere glied, welches bei (a-b)^2 2*a*b ist, nur negativ ist, wenn a positiv ist? (Frage, da gesagt wurde bei der FOrm (a-b)^2 sei im allgemeinen das mittlere Teil immer negativ

https://youtu.be/mpqc4jGhkN8?si=jKnfyirLhieGBFQQ in minute 6:45 behauptet dieser Grünschnabel, dass jede Zahl und er betont absolut jede durch eine Primzahl teilbar sei…

was ist dann mit der 1?