Wie komme ich auf dieses Ergebnis? Fos abi?
Hallo, ich bin gerade am Üben für mein Mathematik Abitur.
Ich verstehe nicht, wie ich bei der Nummer 2 begründet sollte, dass die Funktion h genau eine Nullstelle besitzt und wie ich auf den Funktionsterm, der in der Lösung angegeben ist, komme sollte.
Außerdem verstehe ich die Nummer 3.2 nicht und kann mir den Lösungsvorgang auch nicht aus der Lösung im Buch herleiten.
Ich wäre super dankbar, wenn mir hier jemand helfen könnte.
Am besten bitte leicht und verständlich erklären, Mathe ist nicht meine Stärke😄




3 Antworten
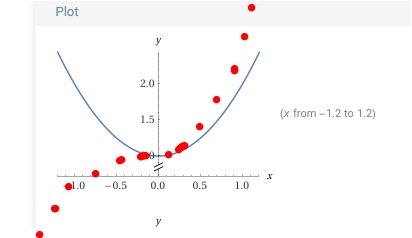
h' , eine Parabel , überall oberhalb der x-Achse
Daher ist die Steigung von h überall positiv
h muss daher die Form punktpunkt haben ( eine von vielen möglich , denn man kann sie nach oben/unten verschieben , h' bleibt genauso

wäre die h' = x² - 4 gäbe es zwei Nullstellen. Und h hätte sowohl pos als auch neg Steigungen
Um es ganz ehrlich zu sagen weiss ich nicht wie ich das besser erklären soll als in der Musterlösung. Wenn du nicht weisst dass wenn f' > 0 für alle x dass f dann streng monoton ist und daher nach der Nullstelle immer größer als 0 sein muss und wenn du nicht weißt wie man aus einer Ableitungsfunktion die Ursprungsfunktion rekonstruiert und dies nicht mal verstehst wenn du schon die Musterlösung hast fehlen dir elementare Grundlagen. Das kann man auch nicht mit
Mathe ist nicht meine Stärke😄
beschönigen, da ist Hopfen und Malz verloren.
Sorry für die deutlichen Worte, aber ich halte nichts davon so etwas zu beschönigen.
alles gut, ich habe nicht vor mathematik zu studieren :)
Achso, bei dem h mit genau einer Nullstelle musst du integrieren also Stammfunktion bilden.
Dann kannst du sagen, dass die Funktion nur eine Nullstelle hat.
Nein. Aus dem Funktionsterm kann man das ablesen durch ausklammern von x (der zweite Teilterm ist dann Nullstellenfrei), aber die erste Teilaufgabe ist unabhängig vom konkreten Funktionsterm zu beantworten.