Mathe Lösung falsch?
Aufgabe:

Lösung laut Lösungsbuch:

Aber ist die Lösung des Lösungsbuches nicht falsch? Wenn ich es per Hand ausrechne kommt bei der Fläche des Fisches ohne den Halbkreis 92/27 raus und wenn ich das dann mit der Fläche des Halbkreises, pi/2, addiere, kommt gerundet 4.98 als Ergebnis raus.

GeoGebra gibt auch 92/27 als Flaeche des Koerpers.
2 Antworten
Du hast offensichtlich die Schnittstelle der beiden Funktionen vernachlässigt und dann das Integral vom 0 bis 4 berechnet. Das ist falsch, wenn nach Flächen gefragt ist.
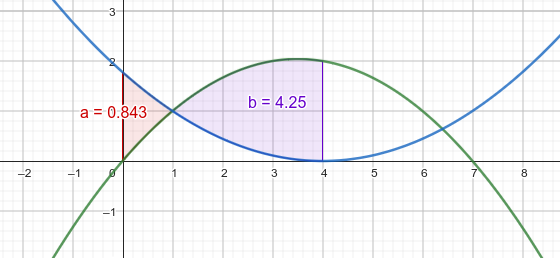
Hier GeoGebra - wenn man es korrekt rechnet:

Zur Erinnerung: Eine Integralberechnung ist keine Flächenberechnung. Sie ist eine Methode zur Flächenberechnung
GeoGebra gibt auch 92/27 als Flaeche des Koerpers.
Nein, eben nicht. GeoGebra zeigt in Deinem Fall den Wert des Integrals an.
Nein. GeoGebra rechnet Integrale aus. Wie aus Integralen Flächen bestimmt werden, muss man schon wissen.
Achso, das wusste ich nicht.
Uns wurde beigebracht, es sei irrelevant, in welcher Reihenfolge wir f und g subtrahieren, solange man Betragsstriche benutzt. Stimmt das also nicht?
Doch, das stimmt schon. Aber diese Aussage hat nichts mit der Schnittstelle zu tun. Das sind zwei Paar Stiefel. Die Betragstriche sorgen nur dafür, dass ein negatives Integral dann als positive Fläche gewertet wird. Berücksichtigst Du die Schnittstelle nicht, dann ist es dafür aber schon zu spät.
Also koennte ich fuer beide Seiten, fuer Intervall 0-1 f(x) - g(x) integrieren und, solange ich es als Betrag nehme, zusammenaddieren, um das korrekte Ergebnis zu bekommen?
hast du durch integriert? oder wie in der Lösung aufgeteilt?
bei der ersten Teilfläche muss man g(x)-f(x) rechnen, bei der zweiten f(x)-g(x)
immer das obere Schaubild minus das untere, im ersten Intervall ist g oben, im zweiten f
wenn man im gesamten Bereich mit f(x)-g(x) rechnet, dann kommt -0.843+4.25 = 3.407 raus, was 92/27 entspricht. Flächen müssen positiv sein, deshalb entweder den Betrag verwenden oder immer obere Funktion minus untere rechnen. Vermutlich ist das dein Fehler
Habe die Betragsstriche vergessen und GeoGebra beachtet die Schnittpunkte nicht, sondern berechnet eben nur das Integral. Habs schon in einem anderen Thread geklaert, trotzdem danke!
Beruecksichtigt Geogebra nicht automatisch die Schnittstellen?