Bestimmung der Nullstellen fer Funktion x^5-x^3?
Die erste Nullstelle ist 0, dass erkenn ich durchs Ausklammern aber was soll ich danach machen?Weil ich versteh nicht ganz wie ich die abc formel dann verwenden soll. Die 2. Und 3. Nullstelle sind anscheinend 1 und -1 aber kann mir bitte einer erklären wie man darauf kommt?
Die lösungen könngen au falsch sein da mein buch oftmals falsche lösungen hat
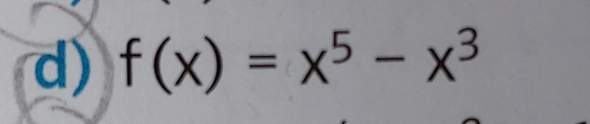
2 Antworten
x^3 * (x^2 - 1) = 0
x^2 - 1 = 0 | + 1
x^2 = 1
Von hier aus kannst du alleine weiter machen.
Man hätte auch die dritte binomische Formel anwenden können:
x^2 - 1 = (x + 1) * (x - 1) = 0
Aber was genau passiert den mit der x^3 die verschwindet einfach
Nein, wegen dem Satz vom Nullprodukt muss nur noch x² - 1 betrachtet werden, weil x³ ja schon dazu geführt hat, dass man die Nullstelle x = 0 gefunden hat.
Genaugenommen ist
x^5 - x^3 = x^3 * (x + 1) * (x - 1) = 0
Mindestens einer der drei Faktoren muss 0 sein. Die Dir schon bekannte Nullstelle x= 0 haben wir hier ignoriert.
x⁵ - x³ = 0 | x³ rausmultiplizieren
x² * x³ - 1 * x³ = 0 | x³ ausklammern
(x² - 1) * x³ = 0 | Satz vom Nullprodukt
(1.) x³ = 0 | dritte Wurzel ziehen
(2.) (x² - 1) = 0 | Klammer auflösen
(1.) x = 0
(2.) x² - 1 = 0 | +1
x² = 1 | zweite Wurzel ziehen
x = ±1
x₁ = -1, x₂ = 0, x₃ = 1
L = {-1; ±0; +1}
Dankee