Wie groß ist dieser Winkel?
Moin,
ich habe hier einen Winkel, dessen Größe ich nicht berechnet bekomme.
Es ist der mit dem "?".
Kann jemand aushelfen?
Danke im Voraus

3 Antworten
Berechnung
c = Wurzel(a^2 + b^2)
c = Wurzel(11^2 + 17,5^2)
c = 20,670027 mm
---
α1 = arctan(a / b)
α1 = arctan(11 / 17,5)
α1 = 32,152295°
---
α2 = arcsin(a1 / c)
α2 = arcsin(10 / 20,670027)
α2 = 28,933378°
---
α = (90° - α1 - α2) * 2
α = (90° - 32,152295° - 28,933378°) * 2
α = 28,914327°

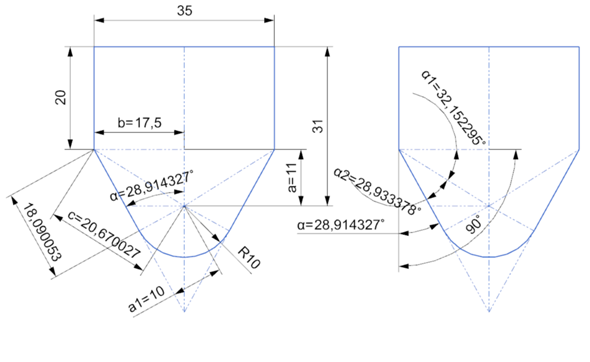
Es gibt ein rechtwinkliges Dreieck mit den Katheten 11 (Bogenmittelpunkt) und 17,5. Die Hypotenuse beträgt 20,67.
Es gibt ein zweites rechtwinkliges Dreieck mit der Hypotenuse 20,67 und der einen Kathete 10. Die zweite Kathete beträgt 18,09. Die Länge der Schräge bis zum Bogenbeginn beträgt 18,9.
In diesen beiden Dreiecken lassen sich die Winkel berechnen, deren Summe von 90° subtrahiert werden muss, um den gesuchten Winkel α zu erhalten.
α = 90° - arctan(11/17,5) - arctan(10/18,09)
α = 28,91°
Die zweite Kathete kann man auch auslassen und statt arctan(10/18,09) sagen: arcsin(10/20,67).
Der Winkel wird sich berechnen lassen, wenn man annimmt, dass die beiden schrägen Linien Tangenten des gedachten Kreises sind, von dem die Rundung ein Teil ist. Wenn man also annimmt, dass der Kreis und die Linien glatt ohne Knick ineinander übergehen. (Die Zeichnung sagt das nicht ausdrücklich, es ist nur eine plausible Annahme.)
Der Radius des Kreises ist mit 10 angegeben, und sein Mittelpunkt liegt da, wo das Maß 31 angibt.
Berechnen muss man nun, wo diese Tangenten den Kreis berühren, dann hat man den gesuchten Winkel.
Als Denkhilfe würde ich die Zeichnung ergänzen: Den ganzen Kreis und die Radien zu den Berührungspunkten einzeichnen.