Welche Dichte hat Methan bei 100bar und 0Grad, wo kann ich das ablesen mit Quellenangabe?
4 Antworten
Dichte von Methan bei 100 bar und 0 °C: ca. 162,66 kg/m³
Quelle: NIST WebBook—>Methane, bei 273,15 K und 10 MPa.
Das kann ich nicht nachvollziehen. Wenn ich die Rechnung mache, sagt er 90.04 kg/m³. Ich habe die erhaltene Graphik in meiner Antwort nachgetragen.
Die Dichte von Methan (CH₄) bei 0 °C und 100 bar ist nicht direkt in den verfügbaren Quellen angegeben. Jedoch lässt sich eine Näherung unter Berücksichtigung der idealen Gasgleichung und der Kompressibilitätsfaktoren vornehmen.
Oder frag chatgpt
Das ist offenbar mit dem idealen Gasgesetz gerechnet, aber mit p=100 atm statt 100 bar. Die Zahl ist also Gurke.
Unter diesen Bedingungen ist Methan ein Gas — flüssiges Methan kann es ja nur unterhalb der kritischen Temperatur geben, die bei Methan −83 °C beträgt.
Die Nullte Näherung ist es, das mit der idealen Gasgleichung zu machen. Wir bekommen ganz einfach mit ρ=m/V und n=m/M (wobei M=16.04 g/mol die molare Masse des Methans ist):

und wenn man da die Zahlenwerte einsetzt, kriegt man ρ=70.6 kg/m³
Andererseits ist es nicht klar, ob Methan unter so hohem Druck noch wirklich wie ein ideales Gas funktioniert. Also greifen wir tiefer in die Trickkiste und nehmen die van-der-Waals-Gleichung. Die wird vorteilhaft mit dem molaren Volumen v=V/n formuliert und das ist günstig, weil wir nur nach v auflösen müssen und dann sofort die Dichte als ρ=M/v erhalten. Die Stoffkonstanten muß man nachschlagen: a=2.253 l²bar/mol² und b=0.04278 l/mol.

Das ergibt eine kubische Gleichung, die man nach der üblichen Methode lösen kann. Wenn man die ganzen Gurkeneinheiten umrechnet, bekommt man v=0.171 l/mol bzw. ρ=M/v=93.7 kg/m³. Das ist also ca. 30% höher als mit der idealen Gasgleichung berechnet, weil die CH₄-Moleküle einander anziehen.
Auch die vdW-Gleichung ist eine Näherung. Ich habe einen online-Calculator für die Gasdichte gefunden, der anscheinend eine Tabelle mit experimentellen Dichten interpoliert; mit dem kriege ich 90.2 kg/m³ heraus, das paßt also ungefähr. Die Einheiten auf dieser Seite machen mich allerdings wieder krank (warum schreiben die bara statt bar?), aber zumindest stimmt das Resultat ungefähr mit dem von mir berechneten überein, und das beruhigt mich sehr, weil ich ehrlich gesagt mit solchen Rechnungen keine Erfahrung habe.
Wenn Du mit der Antwort „knapp über 90 kg/m³“ zufrieden bist, dann sieht das alles recht gut aus.
P.S.: Spaßeshalber habe ich auch Google Gemini gefragt:
What is the density of methane at T=0 °C and p=100 bar?
Die Antwort beginnt mit einer richtigen Bemerkung, nämlich daß man das nicht ideal rechnen kann:
To determine the density of methane at t=0∘C and p=100bar, we should consider that methane will behave as a real gas under these conditions. The ideal gas law, pV=nRT, is not sufficiently accurate at high pressures.We can use the compressibility factor, Z, to account for the deviation from ideal behavior using the modified equation of state:
pV = ZnRT
Er zieht sich dann einen Wert Z=0.8 aus der Nase (bzw. von hier), formt die Gleichung richtig auf ρ=pM/(ZRT) um. Dann setzt er die Zahlenwerte ein, und das muß man sich als Screenshot reinziehen:

Beim Einsetzen im Zähler sind zwei Zehnerpotenzen verlorengegangen, aber beim Formulieren des letzten Satzes stimmt es plötzlich wieder. Wenn wir die Fehlerkompensation nicht hätten, ginge gar nichts mehr. ☺☺
P.P.S.: Noch mehr Spaß mit AI. Ich habe dieselbe Frage an ChatGPT gestellt und im wesentlichen dieselbe Antwort bekommen: Ohne Rechenfehler, aber für mit einem Kompressibilitätsfaktor von Z=0.27, was zu einer Dichte von 262 kg/m³ führt. Auf meine Nachfrage, wo der unrealistisch kleine Z-Faktor herkommt, korrigierte sich das Programm, zog sich Z=0.9 aus irgendeiner Körperöffnung (oder Lücke im Code) und berechnete daraus eine Gasdichte von 78.5 kg/m³.
Da kann man gleich erstsemestrige Studenten fragen. Die haben auch keine Ahnung und streuen ungefähr gleich breit.
3.P.S.: Badbihtch hat das NIST-WebBook ins Spiel gebracht, allerdings kann ich den Zahlenwert nicht nachvollziehen. Wenn ich dort eine isobare Berechnung für Methan anfordere, dann bekomme ich eine Dichte von 90.04 kg/m³.

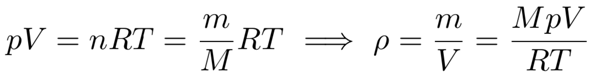
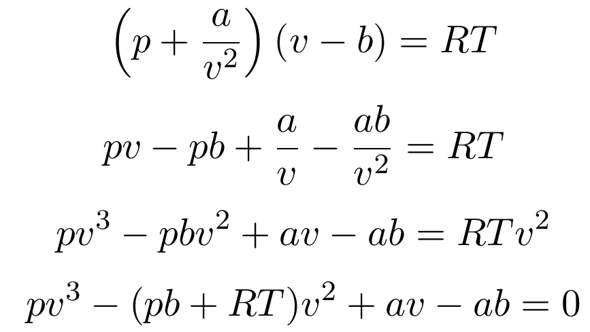

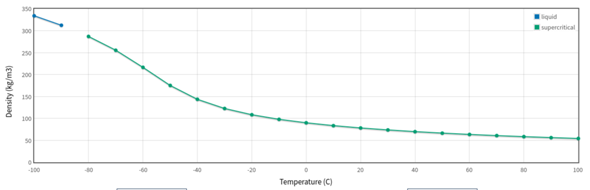
ρ = 90,040 kg/m^3
Quelle:
https://webbook.nist.gov/cgi/fluid.cgi?T=0&PLow=100&PHigh=100&PInc=&Digits=5&ID=C74828&Action=Load&Type=IsoTherm&TUnit=C&PUnit=bar&DUnit=kg%2Fm3&HUnit=kJ%2Fmol&WUnit=m%2Fs&VisUnit=uPa*s&STUnit=N%2Fm&RefState=DEF
(ganzen Link kopieren und einsetzen)
chatGPT hat einen falschen Wert von 71,5kg/m³, es muss aber Gasdatenbanken geben aber wo finde ich die