Quadratische Funktionen?

- Was ist eine quadratische Funktion und welche Darstellungsformen gibt es?

- Was kann man aus der Funktionsgleichung (alle Darstellungsformen) über den Graphen der quadratischen Funktion herauslesen?

- Wie geht man vor, wenn man eine quadratische

Answer 1

[Apilonius64]

Allgemeines

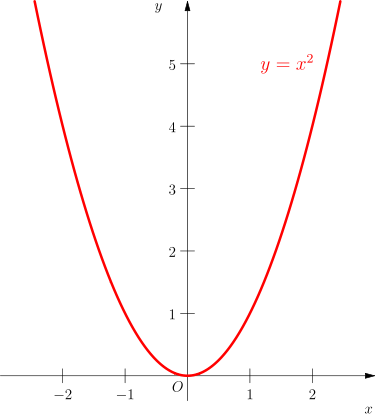
Ich würde jetzt sagen, dass eine quadratische Funktion im Bezug auf einen Graphen meist eine Parabel darstellt. So stellt

$f(x)=x^2$ die Normalparabel da, die ungefähr so aussieht:

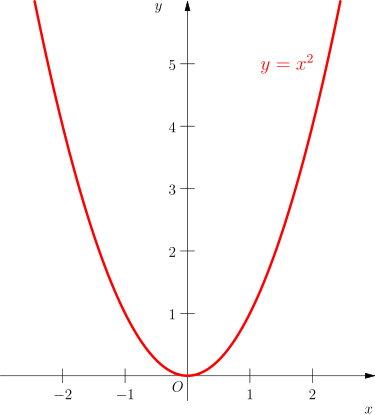
Bildquelle: https://de.wikipedia.org/wiki/Normalparabel#/media/Datei:Parabola2.svg

Nun lassen sich unterschiedlichste Parabeln darstellen. So könnte man die Normalparabel beispielsweise um den Faktor 2 strecken. Dies würde dann

$f(x)=2x^2$ entsprechen. Ist der Faktor negativ, wird die Parabel gespiegelt.

Die Parabel verschieben

Eine verschobene Parabel lässt sich in der Scheitelpunktsform wie folgt darstellen:

$f\left(x\right)\ =\ Streckfaktor\left(x\ -\ VerschiebungX\right)^2+VerschiebungY$

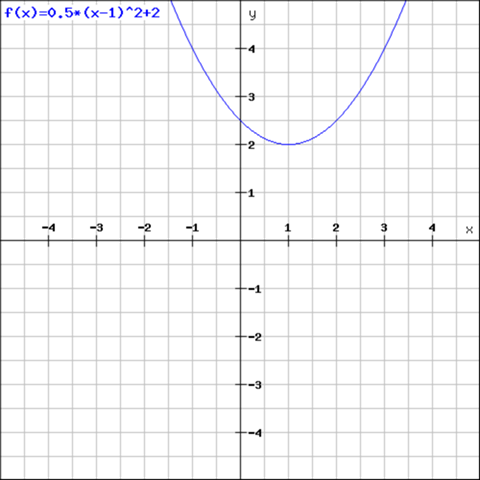
So wäre

$f\left(x\right)\ =\ 0.5(x-1)^2+2$ die Scheitelpunktsform folgender Parabel:

Andere Darstellungsformen

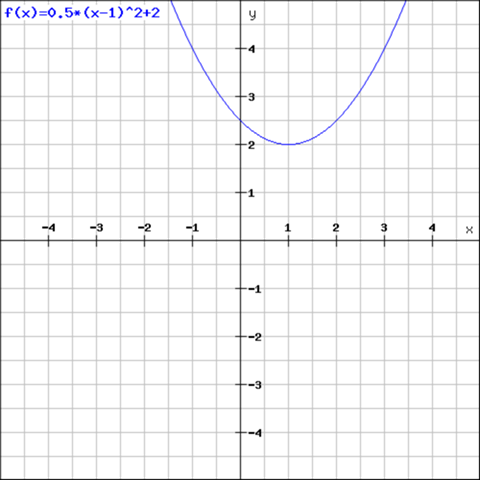
Die Scheitelpunktsform besitzt zwar viele Vorteile, allerdings gibt es auch noch viele andere Darstellungsformen. Hier ein paar im Überblick:

Allgemeine Form

Die allgemeine Form stellt sich wie folgt da: 

$f\left(x\right)=ax^2+bx+c$

Hierbei gilt:

• a = Streckfaktor
• c = Y-Achsenabschnitt

Bei der Umwandlung der Scheitelpunktform zu der allgemeinen Form können in der Regel einfach die Klammern unter der Verwendung der binomischen Formeln aufgelöst werden.

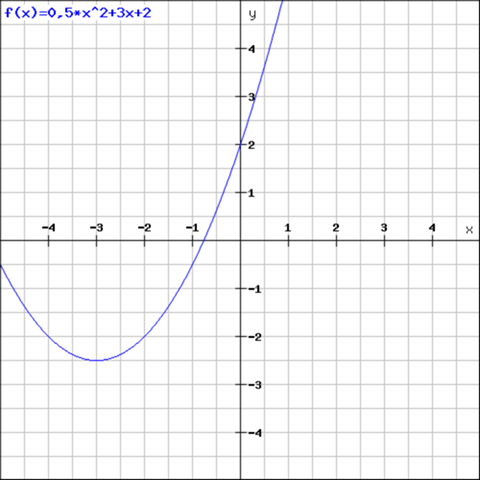
Beispiel:

$f\left(x\right)=0,5x^2+3x+2$

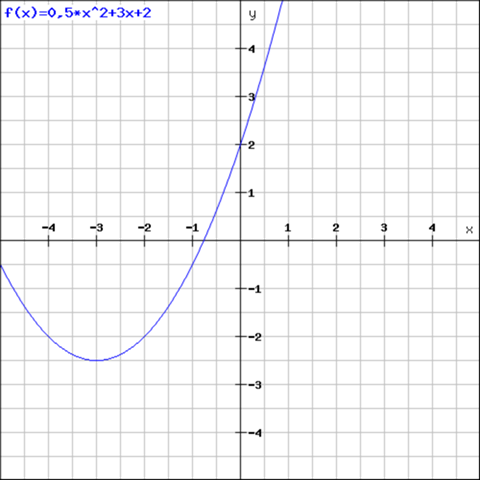
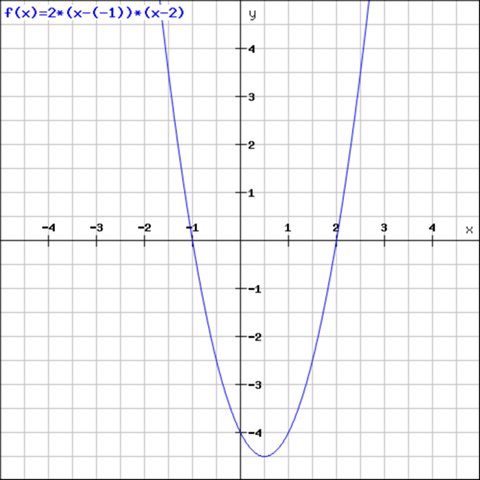
Die faktorisierte Form

Die faktorisierte Form stellt sich wie folgt da

$f\left(x\right)=a\left(x-N1\right)\left(x-N2\right)$ Hierbei gilt:

• a = Streckfaktor
• N1, N2 = Nullstellen

Um die faktorisierte Form zu erhalten reicht es in der Regel aus den Streckfaktor zu bestimmen und die Nullstellen zu berechnen. Hinweis: Für die Darstellung in der faktorisierten Form müssen natürlich auch Nullstellen vorhanden sein.

Beispiel:

$f\left(x\right)=2(x-(-1))(x-2)$ bzw:

$f\left(x\right)=2(x+1)(x-2)$

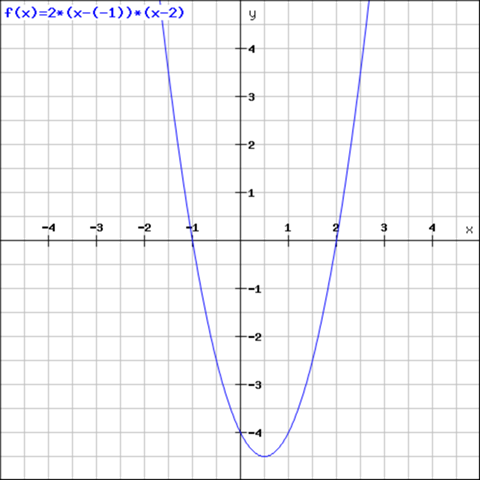
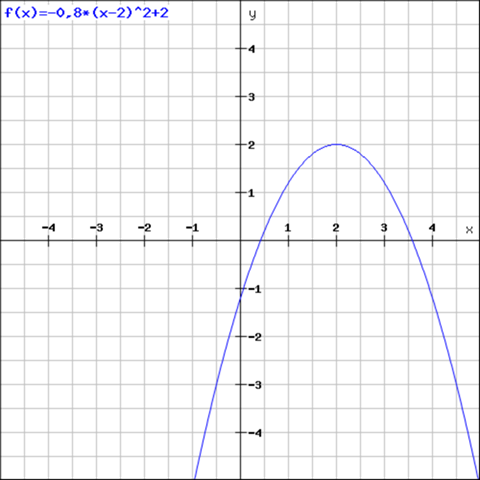
Die Scheitelpunktsform

Die Scheitelpunktform lässt sich wie folgt darstellen:

$f\left(x\right)=a\left(x-b\right)^2+c$ Hierbei gilt:

• a = Streckfaktor
• S(b|c) = Scheitelpunkt

Beispiel:

$f\left(x\right)=-0,8(x-2)^2+2$ Hinweis: Die Parabel ist aufgrund des negativen Streckfaktors gespiegelt.

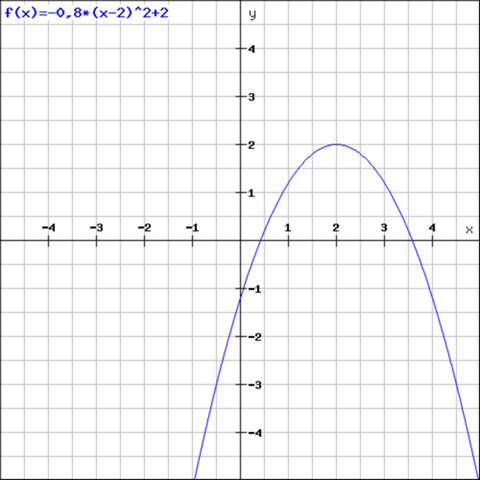
Ich hoffe ich konnte weiterhelfen.

Apilonius

Woher ich das weiß: eigene Erfahrung

Comments

[Monazit]

für meinen Geschmack eine sehr gute Erklärung, übersichtlich, nachvollziehbar und verständlich.

Answer 2

[sarah3]

allgemein ax^2+bx+c

aus c sieht man den Wert von f(0)

Woher ich das weiß: Studium / Ausbildung – Diverses