Pyramide Seiten berechen?
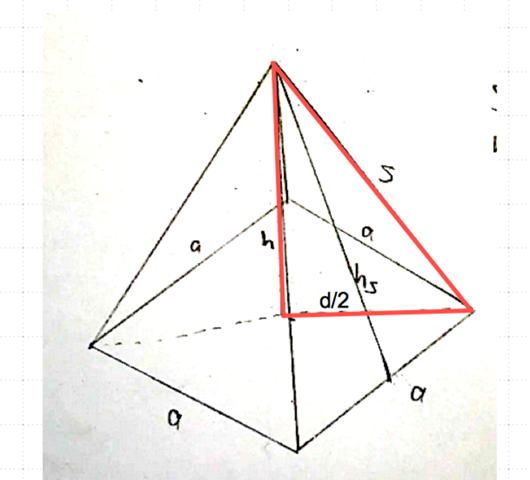
(Bild unten) s und h sind gegeben, wie man die Diagonale rechnet weiß ich auch, aber wie berechne ich jetzt hs. Ich weiß, dass man die Hälfte der Strecke a benötigt aber wie rechnet man diese aus?

4 Antworten
Die Höhe h, die Seite s und die Hälfte der diagonale der Grundfläche bilden ein rechtwinklig es Dreieck. Die Seite s ist dabei die hypotenuse. Mit Satz des Pythagoras kommst du auf die Länge a wenn du danach umstellst. Diagonale im Quadrat ist wurzel(2)*a
zwei Schritte
zuerst a
s² = h² + (a/2 * wurzel(2))²
s² = h² + a²/2
2*(s² - h²) = a²
wurzel(2*(s² - h²)) = a
.
dann hs
hs² = (a/2)² + h²
.
.
Crazy People setzen a² ein
hs² = (a/2)² + h²
hs² = a²/4 + h²
hs² = 2*(s² - h²)/4 + h²
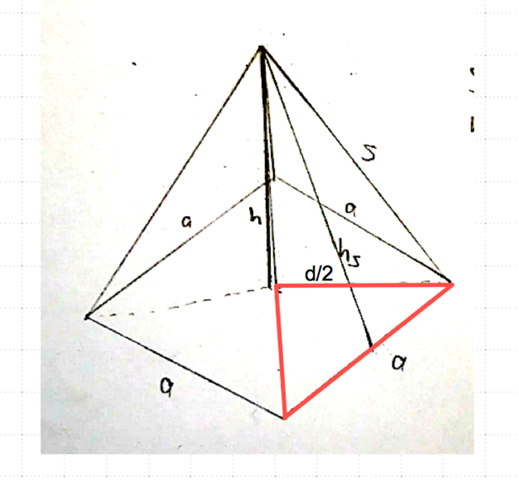
Die Diagonale der Grundfläche und zwei Seitenlängen a bilden ein gleichschenkliges rechtwinkliges Dreieck: 2 a² = d²
1)

(d/2)^2 + h^2 = s^2
(d/2) = √s^2 - h^2
2)

(d/2)^2 + (d/2)^2 = a^2
2 * (d/2)^2 = a^2
a = √2 * (d/2)^2
3)

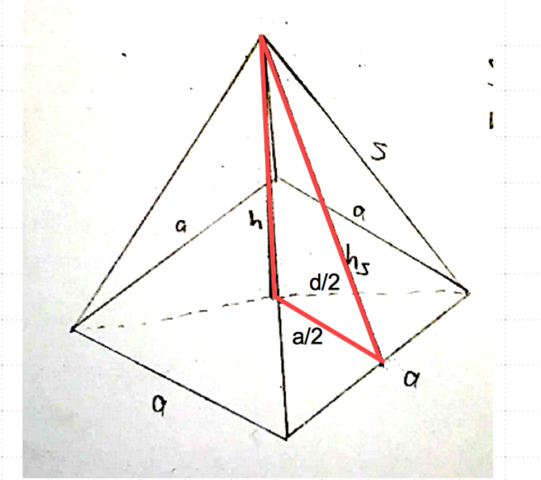
(a/2)^2 + h^2 = hs^2
hs = √(a/2)^2 + h^2