Mathe Hilfe?
Welche Bedingungen brauche ich für die funktionssynthese ?

2 Antworten
Ich sehe auch 5 Bedingungen !
.
.
man hat
f(0) = 0 >>>>> d = 0
f''(6) = 0
f(6) = 72
f(12) = 144
f'(12) = 0
.
0 = 6a*6 + 2b ;
72 = 216a + 36b + 6c + 0 ;
144 = (12³)a + 144b + 12c + 0 ;
0 = 3*144*a + 2*b*12 + c
.
was aber zu einem LGS mit eindeutiger Lösung führt
.

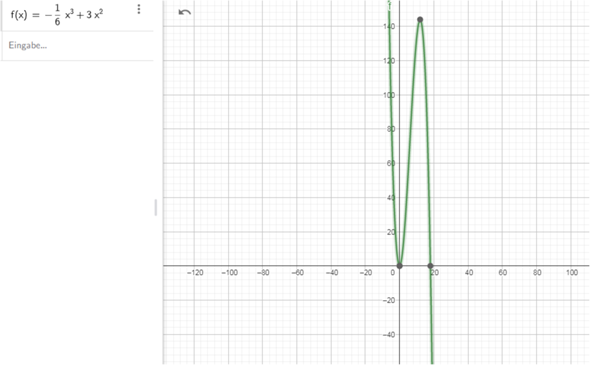
f(x) = -1/6 * x³ + 3 * x²
sie MUSS vier haben , aber mehr sind möglich
Normalerweise sind es auch nur 4
Deine Verwirrung ist also verständlich
Dass man hier mit 5 Bedinungen klar kommen kann , liegt wahrscheinlich daran , dass c und d = 0 sind
Die kann unendlich viele Bedingungen haben. Jeder Punkt ist eine Bedingung. Um eine Funktion dritten Grades eindeutig bestimmen zu können, brauchst Du aber mindestens vier Bedingungen, die voneinander unabhängig sind.
dann wäre das eine Erklärung : man kann beliebig viele Punkte dazu packen
Hallo,
f(0)=0
f(6)=72
f(12)=144
f'(12)=0
f''(6)=0.
Das sind sogar mehr Angaben, als Du brauchst.
Beachte: Kalenderwoche gleich t+8.
Herzliche Grüße,
Willy
Hey, vielen Dank. Ich habe nur eine Unklarheit: Da wir eine Funktion dritten Grades ermitteln sollen, kann sie nicht nur maximal vier Bedingungen haben ?
Nö. Du brauchst mindestens vier Gleichungen. Dürfen aber auch mehr sein. Dann ist das System halt überbestimmt.
Such Dir vier Gleichungen aus und sieh, ob das Ergebnis zum Rest paßt.
Da f(0)=0, fällt der Parameter ohne x sofort flach.
Ja, das habe ich auch bemerkt, aber mich hat verwirrt, dass man eine Funktion dritten Grades ermitteln soll. Diese kann doch nur vier Bedingungen haben, oder nicht ?