Gleichung einer Tangente in einem Punkt?

Hallo, ich bereite mich auf eine Klausur vor und verstehe nicht, wie man die Gleichung einer Tangente in einem bestimmten Punkt am Graphen f bestimmt. Wir hatten noch keine Ableitungsregeln bzw. diese Schritte, wie man die Ableitungsfunktion bildet. Wie soll das ohne jene gehen und was tut man dann?
2 Antworten
Eine Tangentengleichung bestimmen zu sollen, ohne etwas über Ableitungen erfahren zu haben, halte ich für pädagogischen Unsinn. Aber wie der Lehrplan wirklich aussieht, kann ich natürlich aus der Ferne nicht beurteilen.
Die Tangentengleichung von f(x) am Punkt a lautet:
t(x) = f'(a)*(x-a) + f(a)
Beispiel:
Tangente von f(x) = 1/2*x² am Punkt (1,f(1)), d.h. a=1
f'(x) = x
t(x) = f'(1)*(x-1) + f(1)
t(x) = (x-1) + 0.5 = x - 0.5
Vielleicht hilft dir folgender Ausschnitt aus meinem alten Unterrichtskonzept

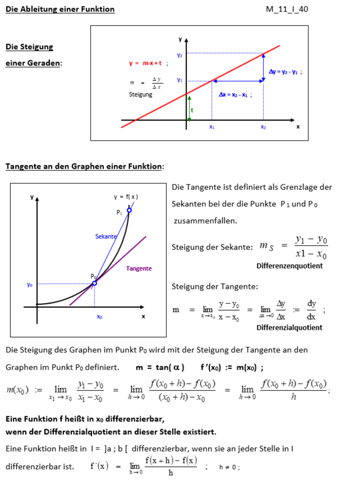
Von der Tangente in welchem Punkt sprichst du hier? Deine Darstellung ist unverständlich. f(x) = 0,5*x^2 => f´(x) = x ; m(Gerade) = f´(1) = 1 ; f(1) = 0,5 ;
Geradengleichung y = x + t ; 0,5 = 1 + t ; => t = - 0,5 ;
Okay also rechne ich den Diffenrenzialquotienten von f(x) aus. Bei f(x)=0,5x² bin ich da auf 1 für die Steigung der Tangente mittels des Diff.quotienten gekommen. Wenn ich die jetzt einsetze und nach dem Achsenabschnitt b umstelle, dann komme ich auf 0,5. Die Gleichung der Tangente solle allerdings f(x)= x-0,5 lauten. Wo kommt das Minus her?