Aufgabe rotationskörper?

Kann mir jemand diese Aufgabe lösen bitte ich verstehe es nicht

Aufgabe 10

Answer 1

[SeifenkistenBOB]

Der Graph soll nicht wie vielleicht sonst üblich um die x-Achse rotieren, sondern um die Gerade y=1. Es ist jedoch wesentlich einfacher, Rotationskörper um die x-Achse zu berechnen, als um eine verschobene Achse. Daher verschieben wir den Graphen der Funktion so, dass er rotationssymmetrisch bezüglich der x-Achse wird. Wir berechnen im Folgenden also den Rotationskörper des Graphen der Funktion

f(x) = 2e^(0.1x) - 1

Die Herleitung der Rotationskörper wurde sicherlich in der Schule besprochen, daher nur kurz angerissen, wie das funktioniert: Wir teilen den Rotationskörper in kleine Kreisscheiben, von denen wir einzeln die Volumina ausrechnen können. Die Funktion f bestimmt den Radius der jeweilen Kreisscheibe, ein x-Achsenabschnitt ∆x die Höhe der Kreisscheibe. Eine einzelne Kreisscheibe hat daher das Volumen (=Kreisfläche*Höhe):

$V_i=\pi\cdot r^2\cdot\Delta x=\pi\cdot\left(f\left(x_i\right)\right)^2\cdot\Delta x$

Für eine gute Näherung muss man nur die x-Achsenabschnitte klein genug wählen und die einzelnen Kreisscheiben aufsummieren.
Für ein genaues Ergebnis wird die Summe in ein Integral überführt:

$V=\int_a^b\pi\cdot f\left(x\right)^2\ \text{dx}$

Funktion einsetzen, Integrationsgrenzen einsetzen und ausrechnen:

$V=\int_0^6\pi\cdot\left(2e^{0.1x}-1\right)^2\text{d}x$

$V=\pi\int_0^64e^{0.2x}-2\cdot2e^{0.1x}+1\ \text{d}x$

Das Integral einer Summe ist die Summe der Integrale der einzelnen Summanden.

$V=4\pi\left[\frac{1}{0.2}\cdot e^{0.2x}\right]_0^6-4\pi\left[\frac{1}{0.1}\cdot e^{0.1x}\right]_0^6+\pi\left[x\right]_0^6$

Answer 2

[Halswirbelstrom]

Berichtigung

LG H.

Comments

[Willy1729]

Den Term unter dem Integral mußt Du quadrieren.

Die Formel für das Volumen eines Zylinders ist pi*r²*h.

Hier summierst Du unendlich viele unendlich dünne Zylinder zum Rotationsvolumen.

[Halswirbelstrom]

@Willy1729

Danke für den "Weckruf". Ich bin wieder wach und habe den Fehler berichtigt.

LG H.

[Willy1729]

@Halswirbelstrom

Jetzt paßt alles.

Answer 3

[AusMeinemAlltag]

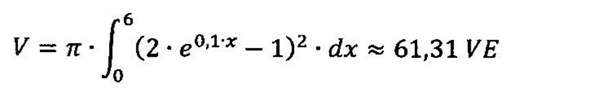
Du must das Integral von ((2 * e ^ (0.1 * x)) - 1) ^ 2 von 0 bis 6 ausrechnen.

Entweder numerisch oder per Stammfunktion.

Anschließend multiplizierst du das Ergebnis noch mit der Zahl Pi.

Comments

[Sweetdreams264]

Aber warum -1

[Willy1729]

@Sweetdreams264

Weil die Formel die Rotation um die y-Achse voraussetzt. Da hier um y=1 rotiert werden soll, verschiebst Du den Graphen einfach um eine Einheit nach unten. Das ergibt letztlich das geforderte Volumen.