Hallo!
Ich möchte gerne wissen, wie ich das Volumen eines Kegelstumpfes berechne, wenn nur die Höhe und der Grundkreisradius angegebn sind.
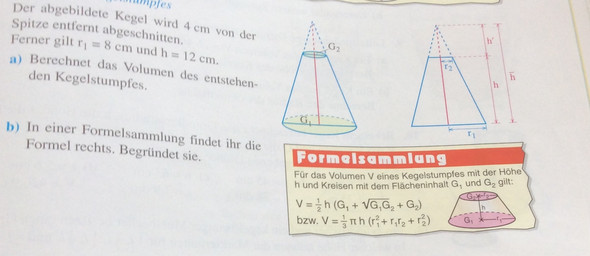
Der Kegel ist ursprünglich 16 cm hoch, wurde aber 4cm unter der Spitze abgetrennt, dazu ist noch der Grundkreisradius von 8cm angegeben. Allerdings ist die mir einzig bekannte Formel zum Berechnen des Volumen eines Kegels so, dass ich den Flächeninhalt der 2 (kleineren) Grundkreisflächd wissen muss. Diese kann ich aber nicht berechnen, weil ich nur eine Angabe kenne, nämlich die 4cm Höhe des kleinen Kegels.
Die Höhe der Seitenfläche des kleinen Kegels lässt sich nicht berechnen, da ich um die Seitenfläche des Kegelstumpfes berechnen zu können und später die Gesamthöhe der Seitenfläche abziehen zu müssen, damit ich die Differenz kenne wissen muss welche Maße der Radius der zweiten Grundfläche hat. Diese müsste ich dann vom Grundkreisradius abziehen, damit ich mithilfe des Satz des Pythagoras die Seitenfläche berechnen kann.
Fakt ist, dass ich zum Berechnen der Seitenfläche des Kegelstumpfes nur die Höhe kenne (12cm).
Wie zur Hölle soll ich dann bitte das Volumen des Kegelstumpfes berechnen?!
Bitte helft mir, denn unser Mathelehrer hat uns keine Formel zur Berechnung genannt.
Wie lautet die Formel die ich anwenden muss?