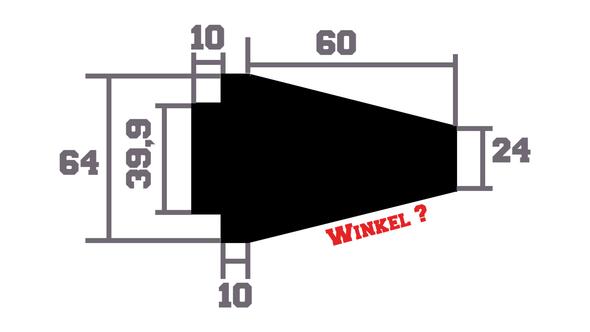
Luftwiderstand beim Kegel?
k habe jetzt ein paar Fragen mir ist das noch nicht wirlich klar, also cw ist umgeformt :
c_w=(2xmxg)/rhoxAxv^2
v habe ich gemessen, A ist soweit ich weiß nicht die Mantelfläche, sondern quasi pi mal r^2. R ist der radius der Öffnung vom Kegel. rho bleibt auch immer gleich.
Ich soll herausfinden wie c_w vom Öffnungswinkel abhöngt. Ich habe einige Kegel gemacht wo der radius jedoch immer gleich bleiben soll, also A auch, und sic nur der Öffnungswinkel ändert. Jetzt stell ich mir die Frage was sich denn ändert bei den verschiedenen Öffnungswinkeln. Es bleibt doch alles gleich bis auf die Masse denn der spitzere Kegekl wiegt bei mir mehr, das würde doch heißen das sich die nur die masse und der die geschwindigkeit ändert.
Was würdet ihr denn bei der Frage "Wie hängt der Luftwiderstandsbeiwert cw vom Öffnungswinkel des Kegels ab" antworten?