Wie löst man diese Matheaufgabe (Volumen)?
Wer mag, 6-8. Sind nicht so arg schwere Aufgaben, aber ich bin gerade eh auf Gutefrage.

2 Antworten
Aufgabe 7a
Berechnung Volumen Hammerkopf
---
Dreieckprisma Volumen V1
V1 = (( c² * Wurzel(3) ) / 4) * c
V1 = (( 3^2 * Wurzel(3) ) / 4) * 3
V1 = 11,691343 cm³
---
Quader Volumen V2
V2 = c² * d
V2 = 3^2 * 5
V2 = 45 cm³
---
Pyramide Volumen V3
V3 = c² * a / 3
V3 = 3^2 * 1 / 3
V3 = 3 cm³
---
Bohrung Volumen V4
V4 = (b/2)² * pi * c
V4 = (2/2)^2 * pi() * 3
V4 = 9,424778 cm³
---
Hammerkopf Volumen V
V = V1 + V2 + V3 - V4
V = 11,691343 + 45 + 3 - 9,424778
V = 50,266565 cm³
------------
Aufgabe 7b
Masse = V * ρ
Masse = 50,266565 * 7,86
Masse = 395,095g

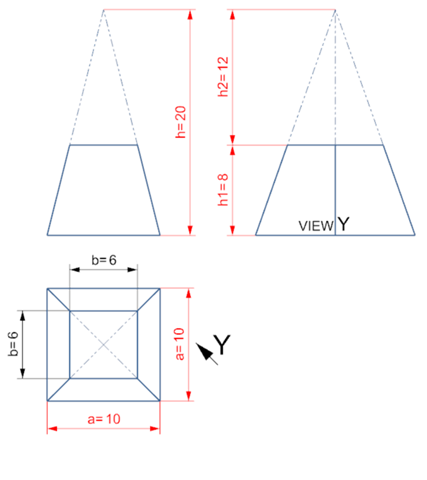
Aufgabe 6
Grundkante a:
V = a² * h / 3
a = Wurzel(3 * V / h)
------
Doppeltes Volumen:
2 * V = a² * h / 3
a = Wurzel(2) * Wurzel(3 * V / h)
a mit Wurzel(2) multiplizieren, um das Volumen zu verdoppeln.
------
Halbes Volumen:
(1 / 2) * V = a² * h / 3
a = (1 / Wurzel(2)) * Wurzel(3 * V / h)
a durch Wurzel(2) dividieren, um das Volumen zu halbieren.
------------
Aufgabe 8a
b -- Berechnung mit Strahlensatz
12 / 20 = b / 10
b = 12 / 20 * 10
b = 6 m
------
Aufgabe 8b
Volumen V Pyramidenstumpf
V = (h1 / 3) * (a² + (a * b) + b²)
V = (8 / 3) * (10^2 + (10 * 6) + 6^2)
V = 522,666667 m³

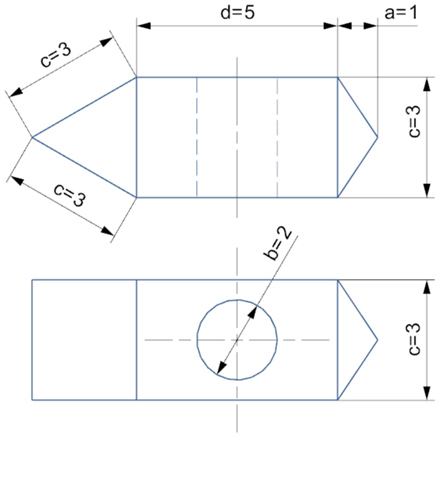
Für 7a zerlegst du den Hammerkopf in einzelne Körper (es sind 3), deren Volumen du berechnen kannst, und addierst sie. Von diesen Volumen ziehst du das Volumen des Loches/Zylinder, musst du auch berechnen, ab.
Für 7b multiplizierst du das in 7a berechnete Volumen mit der Dichte.