Wie berechnet man die Nullstelle von Brüchen?
Wie berechne ich die Nullstelle von 1/9x²?
Es ergibt sich folgendea Problem :
1/9x²=0. |-1/9
X²=-1/9
An der Stelle sollte man die wurzel ziehen, damit X alleine steht. Geht aber schlecht. Was tun?
3 Antworten
Wenn du nicht den Formeleditor verwendest verwende bitte Klammern damit man weiß dass das x^2 nicht im Nenner steht.
Wieso ist das 1/9 auf der linken Seite weg wenn du es auf beiden Seiten subtrahierst?
Über diesen Ansatz kommst du sicher nicht weiter.
Warum verwendest du nicht den Satz vom Nullprodukt?
Ein Produkt (hier das Produkt aus 1/9 und x^2) ergibt Null, wenn einer der Faktoren 0 ergibt. Seit wann ist 1/9 = 0? Der Term wird nur für einen Wert = 0.
Also ich kenne das so, jedenfalls hat mein Lehrer mir das so bei Zahlen gezeigt, die keine Brüche sind. Sonst habe ich damit immer richtige Ergebnisse erzielt. Ich habe es gleich null gesetzt und berechnet. Eine Funktion kann ja auch zwei Nullstellen haben.
1/9x=0
x=-1/9
Wie kommst du darauf?
1/9 bekommst du nicht vom x weg, indem du 1/9 subtrahierst.
Multipliziere doch mal mit 9, danach ist 1/9 nämlich "weg":
1/9•x = 0 |•9
9•1/9•x = 9•0
x = 0
Ah ja. Und wann ist nun 1/9 = 0? Du hast keine FUnktion hingeschrieben, sondern einen Term. Die Funktion f(x) = (1/9)*x^2 hat keine zwei Nullstellen, sondern nur eine. Offensichtlich hast du von den Erklärungen die dir dein Lehrer gegeben hat nicht viel verstanden, sorry dass ich das so offen sage.
Ich kenne das halt so von Nicht-Brüchen, dass man das so macht. Hier ein Beispiel von Mathematrik https://youtu.be/oywjcZxfwS4
Wie berechne ich die Nullstelle von 1/9x²?
Eine Menge falsche Antworten stehen da :-(
(1/9) · x² = 0
Nun multiplizierst du die Gleichung mit 9 und bekommst.
x² = 0
Da ziehst du die Wurzel und erhältst:
x = 0
Wenn ich die Frage richtig interpretiere, lautet die Aufgabe (1/9) · x² = 0.
An Antworten las ich hier unter anderem die Lösung x²=-1/9 (vom Fragesteller) sowie die Aussage, dass es gar keine Nullstellen gibt.
Deine Antwort ist natürlich korrekt.
Die Antwort x = 1/9 kam vom Fragesteller und die andere falsche Antwort habe ich bereits korrigiert.
Hi,
da hast Du falsch angefangen, aber zuerst mal die Frage heißt es:
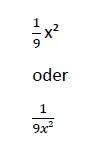
Dann sehen wir weiter?
LG,
Heni
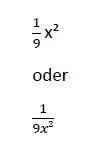
OK!
Dann:
(1/9) * x² = 0
Satz vom Nullprodukt anwenden,
1/9 kann niemals 0 sein,
also x² = 0 | Wurzel ziehen
Ergibt als einzige Lösung, x = 0
Ich dachte null setzen und dann so:
x(1/9x)
X=0
1/9x=0
1/9=x
Weil mein Lehrer hat mir gesagt, dass man alles null setzen muss. Bis jetzt habe ich immer damit richtige Ergebnisse erzielt. Nur bei Brüchen kommt bei der Methode immer was falsches raus. Ich guck mir auch immer die Videos von Mathematrik an, und die hat das auch immer so gemacht.
So, wie das hier gemacht wurde https://youtu.be/oywjcZxfwS4
Na ja, man kann auch diesen Weg gehen, aber dann machst Du wieder einen Fehler:
1/9 x = 0 ist dann auch wieder nur die Lösung x = 0.
Wieder Nullprodukt verwenden und Du bekommst erneut die Lösung x = 0;
Demnach ist nur die eine Lösung x = 0, (doppelte Nulllstelle)
NEIN! Nur wenn es heißt : x + 1/9 = 0, nicht bei 1/9x = 0, das ist ein Unterschied!
Also quasi x(1/9x)
X=0
1/9x=0
x=-1/9
So geht doch der Satz vom Nullprodukt.