Symmetrie bei Funktionen?
Wenn es bei einer ganzrationalen Funktion gerade UND ungerade Exponenten gibt, hat es dann gar keine Symmetrie?
5 Antworten
Eine Funktion mit ungeraden und geraden Potenzen kann z.B. symmetrisch zur Achse x=a sein.
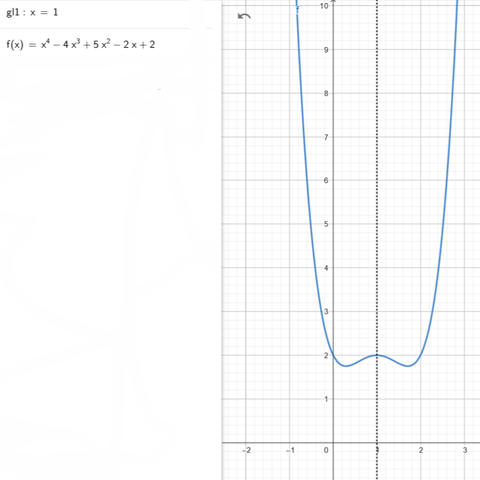
Beispiel: f(x) = x^4 - 4x^3 + 5x^2 - 2x + 2 verläuft symmetrisch zur Achse x=1

ich kanns nicht beweisen : Aber mir scheint , es müssen alle Exponenten vorhanden sein ( außer der Konstante )
Doch , es kann dann Punktsymmetrie geben . Aber nicht zu (0/0) , dem Ursprung

ist f(x) = (x-3)³ ..............die um 3 nach rechts verschobene f(x) = x³ . Die ist nun punktsym zu (3/0)

Wenn eine Funktion sowohl gerade als auch ungerade Exponenten hat, ist sie in der Regel weder symmetrisch zur y-Achse noch punktsymmetrisch zum Ursprung. Stattdessen kann sie eine kombinierte Symmetrie aufweisen.
Wenn mich nicht alles täuscht sagt man in so einem Fall einfach : ,,keine erkennbare Symmetrie‘‘
So ist es.