Schwerpunkt einer Fläche mit Integral?
Hallo. Wie berechne ich von der Fläche, die durch f(x) und g(x) gebildet wird, den Schwerpunkt in x-Richtung.
f(x)=-(x+4)^2 +4 g(x)=x^3
Also 1/A • Integral (von 0-1,562) [xy] …
Muss man dann x • (f(x)-g(x)) rechnen oder g -f oder f-0 oder was?
Dankö

2 Antworten
Nutzer, der sehr aktiv auf gutefrage ist
Der Schwerpunkt [xS, yS] einer durch f(x) abgegrenzten Fläche im Intervall [a,b] ergibt sich folgendermaßen:

In der Aufgabe ist dann f() durch die Differenzfunktion f()-g() zu ersetzen.
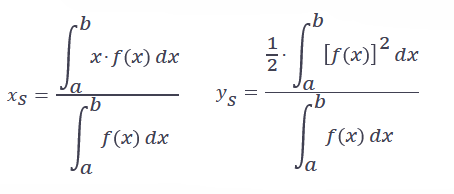
Also 1/A • Integral (von 0-1,562) [xy] …
Du musst einfach in die hier gemeinte Formel einsetze.
aber dann f-g?