Mathe frage- Begründung hierfür?
Ich habe gerade das Integral von der ln Funktion von 0 bis e ausgerechnet. Und ich habe mich gewundert, dass da 0 raus kommt.
Wie ist dafür die geometrische Erklärung ? Ich find das irgendwie magisch, weil die ln Funktion ja so gegen unendlich beim gegen gehen geht, aber das integral von 0 bis e ist Null…
3 Antworten
Der Graph von ln(x) geht zwar für x gegen 0 gegen minus unendlich, allerdings schmiegt er sich dabei sehr schnell an die y-Achse, so dass die Fläche unterhalb der x-Achse endlich ist. Der Stammfunktion x ln(x) - x sieht man die Werte für die Intervallgrenzen (x gegen 0 und x = e) direkt an.
Bildlich sind Integrale als Flächen interpretierbar

dabei sind die Fläche UNTER der x-achse negativ , oberhalb positiv
Und die Fläche von 0 bis 1 ist neg und genauso groß wie die Fläche von 1 bis e, die aber pos.
Deswegen muss man bei Flächenbestimmungen immer erst prüfen ,ob sich im Intervall Nullstellen befinden
.
Auch hier

bei -2 bis + 2 ist das Integral Null , die Fläche aber zwei -2 bis 0 oder 0 bis +2
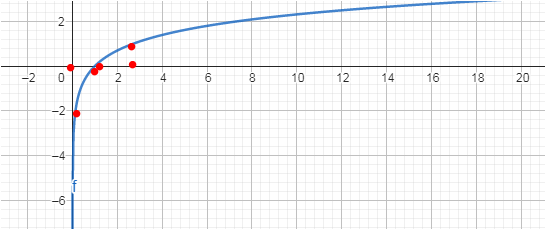
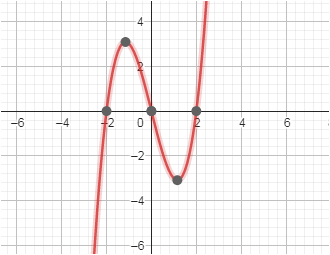
Integralfläche über der x-Achse ist positiv, die drunter negativ. In der Summe Null.
Warum die obere Fläche genau so groß wie untere bis e ist?
Warum genau bei e die Flächenbilanz null wird möchte ich wissen. Wieso nicht bei 27 oder 12 oder 4?
Es ist Logarithmus naturalis, also zur Basis e.
….Genau. Das habe ich ja genau so ausgerechnet.
aber hinter so einem Rechenergebnis muss ja irgendeine Geometrie liegen. null, e und null sind ja drei nicht so unbesondere Zahlen.