Lösung dieses Integrals?
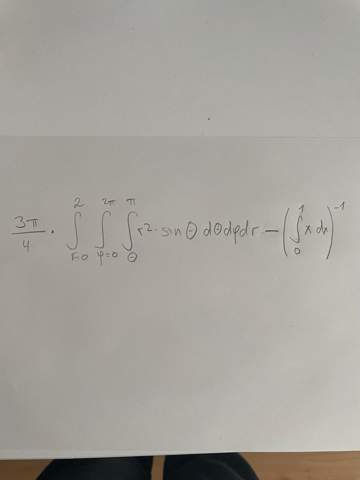
Hallo, wie würde man dieses Integral lösen?
lg
1 Antwort
Der erste Integrand kommt mir bekannt vor. Es ist das Volumeninfinitesimal einer Kugel. Leider ist es nicht richtig sauber formuliert. Die Untergrenze des innersten Integrals hat nur den griechischen Buchstaben gross_theta abbekommen aber nicht den obligatorischen Zahlenwert. Ich war so frei und habe hier den Wert 0 angesetzt.
Sollte die Untergrenze wirklich nur mit gross-theta markiert werden, dann müsste das Integral so interpretiert werden, dass gross-theta variabel bleiben soll. Dann müsste man von der Anschauung ausgehen, dass das Volumen einer Kugel mit Kegelausschnitt berechnet werden soll. Ist das hier verlangt?
Die Berechnung einer Vollkugel gestaltet sich so:
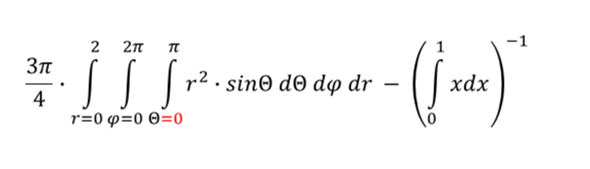
Berchnung des innersten Integrals und parallel Berechnung des letzten Integrals
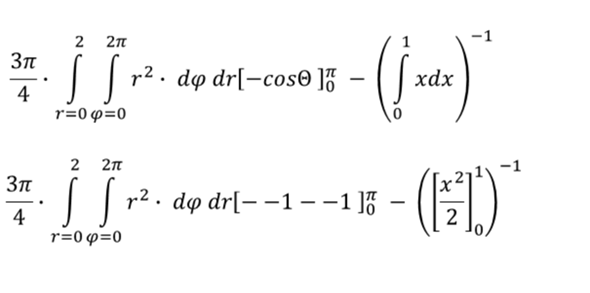
Der Integrand enthält kein phi. Darum darf der Faktor 2*pi eingeführt werden. Die weiteren Rechenschritte sollten nachvollziehbar sein.

Kürzen der roten Faktoren führt zu folgenden Zahlenwert:

Hier würde mich interessieren, wodurch dieses bestimmte Integral motiviert ist? Gibt es einen physikalisch-technischen Hintergrund, der zu so einem Ergebnis führt?
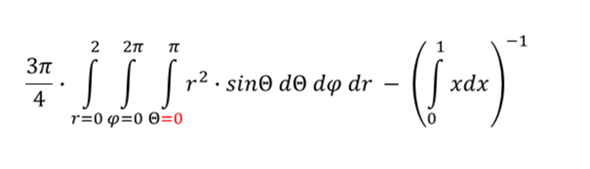
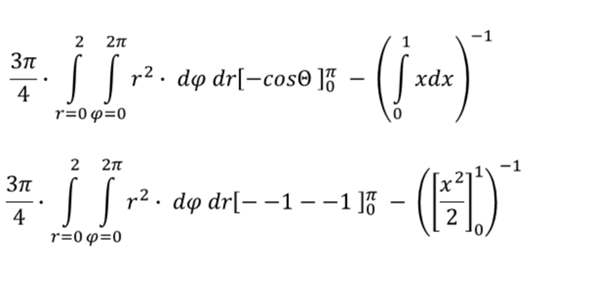


Interessant. Aber ein Integral, in dem der Integrand ein infinitesimales Kugelvolumenelement darstellt als Lösung eines Parkettierungsproblems? Das glaube ich nicht.
Ok Chef ist gemacht…hatte ich eh nur vergessen…
ich versteh auch nicht ganz warum hier das Volumenintegral einer Kugel bei zweidimensionalen, rechteckigen Fliesen steht
hier kriegste auch noch hilfreichste Antwort
das war tatsächlich ne knobelaufgabe: der Boden einer Turnhalle soll mit Fliesen gedeckt werden welche aus rechteckigen Fliesen mit Seitenverhältnis 23:11 sowie quadratischen Fliesen unbekannter Seitenlönge bestehen. Die Aufgabe besteht daher darin, die Seitenlänge des Quadrats zu finden und das obige Integral ist die Lösung davon. Ich hab allerdings keinen Plan wie man drauf kommt