Integral?
Wie löse ich das Integral? Ist das was für den Residuensatz?
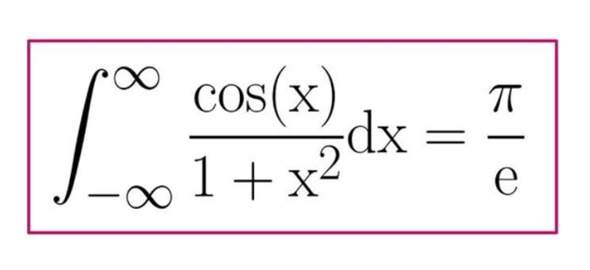
3 Antworten
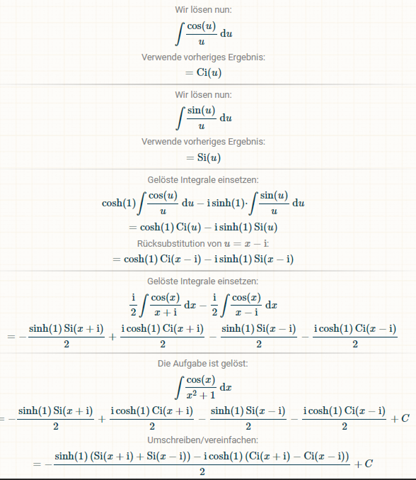
Well... Für die Stammfunktion gäbe es den Weg von TBDRM: https://www.integralrechner.de/#expr=cos%28x%29%2F%281%2Bx%5E2%29 (Schritt für Schritt Hherleitung)



(Si = Integralsinus und Ci = Integralkosinus)
Das kann man bestimmt auch leichter mit Clausen-Funktionen lösen, aber egal...
Integralsinus ist Punksymmetrisch zum Ursprung und hat daher für beide Werte mit x -> unendlich als Ergebnis pi/2. Integralkosinus ist stattdessen 0 aka fällt weg aka Lösung:
-sinh(1)pi/2-[...]_{-unendlich}
Minus unendlich gibt und dann für den Kosinus Teil jeweils pi i => 2pi i => cosh(1) pi / 2. Punksymmetrie beim Si macht, dass es 0 ergibt aka:
-sinh(1) pi + cosh(1) pi

Wunder der Mathematik. ;)
Residuenstz:

Quelle: https://www.math.uni-hamburg.de/home/oberle/skripte/komplex/komplex11.pdf




Für den Residuensatz scheint es mir keinen einfachen Ansatz zu geben. Die erste Idee wäre, über den Weg von -N bis N und im Halbkreis obenrum zurück nach -N zu integrieren. Das Integral über den Halbkreis würde man dann nach oben abschätzen wollen, allerdings macht da der komplexwertige Kosinus Probleme.
Als Ansatz hatte ich gesehen, dass man den Cosinus mit e^ix ausgetauscht hatte und danach noch was gezeigt hatte, aber das habe ich nicht so recht verstanden
Du kannst eine Partialbruchzerlegung machen, die Substitution u = x + i durchführen, sowie Additionstheoreme verwenden, was auf den Integralsinus/-kosinus führt, womit du es dann lösen kannst.
Kannst du es mit den Residuensatz machen? Das fände ich cool