Hilfe Mathe fos11 bitte?

Ist das nicht einfach 0,-3, -6

Answer 1

[mihisu]

Ist das nicht einfach 0,-3, -6

Nein. Wie bist du darauf gekommen?

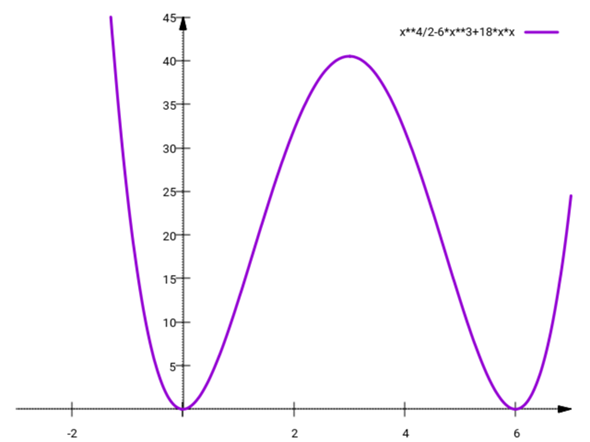
====== a) ======

$f(x)=0\text{,}5\,x^4-6\,x^3+18\,x^2$

$f(x)=0\text{,}5\,x^2\cdot\left(x^2-12\,x+36\right)$

$f(x)=0\text{,}5\,x^2\cdot\left(x^2-2\cdot 6\cdot \,x+6^2\right)$

$f(x)=0\text{,}5\,x^2\cdot\left(x-6\right)^2$

Anhand der Linearfaktorzerlegung kann man nun die folgenden Nullstellen der Funktion f ablesen...

• Nullstelle bei x = 0 mit Vielfachheit 2
• Nullstelle bei x = 6 mit Vielfachheit 2

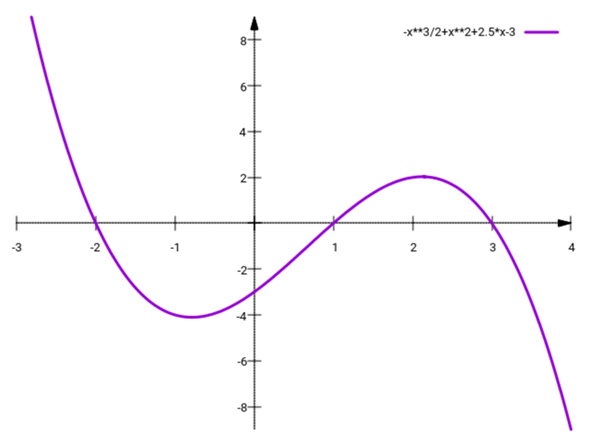
====== b) ======

$f(x)=-0\text{,}5\,x^3+x^2+2\text{,}5\,x-3$

$f(x)=-0\text{,}5\cdot\left(x^3-2\,x^2-5\,x+6\right)$

Erraten einer Nullstelle...

$f(1)=-0\text{,}5\cdot \underbrace{\left(1-2-5+6\right)}_{=0}=0$

Nebenrechnung... Polynomdivision...

 (x³ - 2 x² - 5 x + 6) : (x - 1) = x² - x - 6
-(x³ -   x²          )
----------------------
        -x² - 5 x + 6
      -(-x² +   x    )
      ----------------
             -6 x + 6
           -(-6 x + 6)
           -----------
                    0

$f(x) = -0\text{,}5\cdot \left(x-1\right)\cdot \left(x^2-x-6\right)$

Nebenrechnung mit quadratischer Lösungsformel (Mitternachtsformel)...

$x^2 - x - 6 = 0\quad \Leftrightarrow\quad x=\frac{-\left(-1\right)\pm\sqrt{\left(-1\right)^2-4\cdot 1\cdot \left(-6\right)}}{2}$

$\quad \Leftrightarrow\quad x=\frac{1\pm\sqrt{1+24}}{2}$

$\quad \Leftrightarrow\quad x=\frac{1\pm\sqrt{25}}{2}$

$\quad \Leftrightarrow\quad x=\frac{1\pm 5}{2}$

$\quad \Leftrightarrow\quad x=\frac{1+ 5}{2}=3\quad \vee\quad x=\frac{1-5}{2}=-2$

$f(x)=-0\text{,}5\cdot \left(x-1\right)\cdot\left(x-3\right)\cdot \left(x+2\right)$

Anhand der Linearfaktorzerlegung kann man nun die folgenden Nullstellen der Funktion f ablesen...

• Nullstelle bei x = 1 mit Vielfachheit 1
• Nullstelle bei x = 3 mit Vielfachheit 1
• Nullstelle bei x = -2 mit Vielfachheit 1

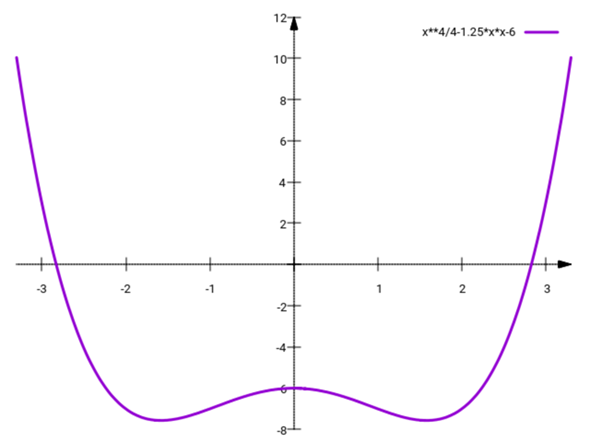
====== c) ======

$f(x)=0\text{,}25\,x^4-1\text{,}25\,x^2-6$

$f(x)=0\text{,}25\cdot \left(x^4-5\,x^2-24\right)$

Die entsprechende biquadratische Gleichung zur Berechnung der Nullstellen lässt sich [unter anderem mit Hilfe der quadratischen Lösungsformel (Mitternachtsformel)] beispielsweise folgendermaßen lösen...

$x^4-5\,x^2-24=0 \quad \Leftrightarrow\quad \left(x^2\right)^2-5\,x^2-24=0$

$\quad \Leftrightarrow\quad x^2=\frac{-\left(-5\right)\pm \sqrt{\left(-5\right)^2-4\cdot 1\cdot \left(-24\right)}}{2\cdot 1}$

$\quad \Leftrightarrow\quad x^2=\frac{5\pm \sqrt{25+96}}{2}$

$\quad \Leftrightarrow\quad x^2=\frac{5\pm \sqrt{121}}{2}$

$\quad \Leftrightarrow\quad x^2=\frac{5\pm 11}{2}$

$\quad \Leftrightarrow\quad x^2=\frac{5+11}{2}\quad \vee\quad x^2=\frac{5-11}{2}$

$\quad \Leftrightarrow\quad x^2=8\quad \vee\quad x^2=-3$

[Hier könnt man nun zwischendurch f(x) = 0,25 ⋅ (x² - 8) ⋅ (x² + 3) erkennen. Für jede relle Zahl x ist der Faktor (x² + 3) größer oder gleich 3, also insbesondere immer postiv, also insbesondere ungleich 0. Der Faktor (x² - 8) lässt sich hingegen entsprechend der dritten binomischen Formel in (x - √(8)) ⋅ (x + √(8)) zerlegen. Ansonsten kann man aber auch erst einmal folgendermaßen beim Lösen der Gleichung weiterarbeiten...]

$\quad \Leftrightarrow\quad x^2=8\quad \vee\quad \underbrace{x^2=-3}_{\text{keine reelle Lösung}}$

$\quad \Leftrightarrow\quad x^2=8$

$\quad \Leftrightarrow\quad x=\pm\sqrt{8}$

$f(x)=0\text{,}25\cdot \left(x-\sqrt{8}\right)\cdot \left(x+\sqrt{8}\right)\cdot \left(x^2+3\right)$

Anhand der Zerlegung kann man nun die folgenden reellen Nullstellen der Funktion f ablesen...

• Nullstelle bei x = √(8) mit Vielfachheit 1
• Nullstelle bei x = -√(8) mit Vielfachheit 1

Comments

[indiachinacook]

Vielfachheit

Sagt man das heutzutage so? Ich bin mir sicher, daß das bei uns in der Schule Multiplizität hieß.

[meeeps]

@indiachinacook

Hab ich schon mal gehört. Sagt man halt in der oberstufe glaube.

[mihisu]

@indiachinacook

Ja. „Vielfachheit“ ist da der Audruck, der mir am häufigsten in diesem Zusammenhang begegnet ist (insbesondere in der Schule).

Man spricht ja auch meist von „einfachen Nullstellen“, „doppelten Nullstellen“, „dreifachen Nullstellen“, „vierfachen Nullstellen“, etc. Da steckt also die „Vielfachheit“ auch in diesen Formulierungen.

An der Universität (und im Internet, beispielsweise bei Wikipedia) sind mir neben „Vielfachheit“ aber auch die Begriffe „Multiplizität“ und „Ordnung“ in diesem Zusammenhang begegnet, je nachdem, was der jeweilige Dozent gerade bevorzugt hat. Aber „Multiplizität“ ist mir dabei deutlich am seltensten begegnet.

Answer 2

[indiachinacook]

• ½x⁴−6x³+18x² = ½x²(x²−12x+36) = ½x²(x−6)² ⟹ x = 0⁽²⁾ ∨ 6⁽²⁾
• −½x³+x²+2½x−3 = −½(x−2x²−5x+6) = −½(x−1)(x−3)(x+2) ⟹ x = 1 ∨ 3 ∨ −2
• ¼x⁴−1¼x²−6 = ¼(x⁴−5x²−24) = −¼(x²−8)(x²+3) ⟹ x = ±√8 = ±2√2 ∨ ±√3i

Die erste Gleichung hat also zwei reelle Doppellösungen, die zweite drei reelle Ein­fach­lösungen und die dritte hat zwei reelle und zweite komplexe Lösungen, alle einfach.

Ich werfe Dir noch die Funktionsgraphen dazu:

Die Doppellösungen sind natürlich zugleich Nullstelle und Extremum.

Answer 3

[gauss58]

a) x² ausklammern und quadratische Gleichung lösen

b) eine Nullstelle raten, x = 1 ist erkennbar, Polynomdivision und quadratische Gleichung lösen

c) Substitution x² = z und zunächst quadratische Gleichung lösen