Habe ich die Funktionsgleichung richtig aufgestellen?
Hi, ich habe mal wieder eine Frage zu Mathe. Meine Arbeit wurde verschoben und ich schreibe sie wahrscheinlich morgen 🥺
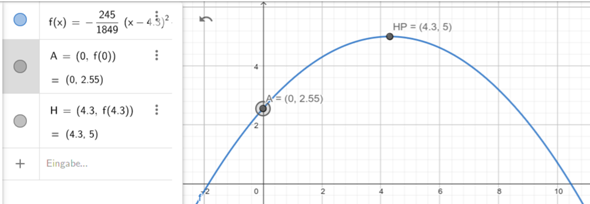
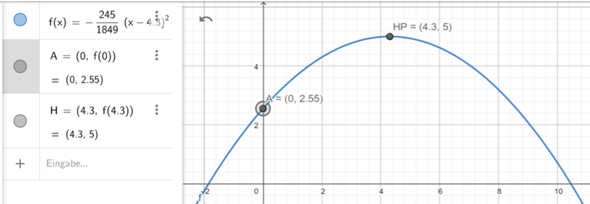
Beim Volleyball steht der Volleyball Spieler 9 m von dem 2,43 m hohen Netz entfernt. Das Spielfeld ist insgesamt 18 m lang. Beim Aufschlag des Spielers wird der Ball in Höhe von 2,55 m getroffen. Den höchsten Punkt erreicht der Ball 4,3 m vom Volleyballspieler entfernt mit einer Höhe von 5 m. Stelle eine Funktionsgleichung auf, deren Graf den Abschlag modelliert.
Ich hatte nun als Lösung:
f(x)=-0,13(x-4,3)²+5
(wir runden auf die zweite Nachkommastelle)
Nun wollte ich fragen, ob ich die richtige Lösung rausbekommen habe, da ich leider sonst über keine Mittel verfüge, es zu kontrollieren.
Vielen, vielen Dank und einen schönen Tag 🫶🏻, LG Luzie822🙃
3 Antworten
Passt: Du hast den Scheitelpunkt S(4,3|5) gegeben (wenn der Aufschlag sinnvollerweise auf die y-Achse gelegt wird, wie Du es gemacht hast) und kennst einen weiteren Punkt, nämlich den Aufschlagpunkt P(0|2,55).
In die Scheitelpunktform S und P eingesetzt, kommt auch Dein Streckungsfaktor -0,13 (gerundet) raus.
Deine Parabel ist unter Berücksichtigung der Rundungsregel schon korrekt. Ich würde allerdings in solchen Fällen die korrekte Lösung mit dem Streckfaktor
bevorzugen.
Ich bekomme für a=-0,27 raus,
also f(x )= -0,27(x-4,3)²+5
Doch, du kannst eine Probe machen. Du kennst den Abschlagpunkt, also den Punkt für x=0 , der ist (0/2,55).
Du setzt x=0 und mußt dann 2,55 rausbekommen.
deinen Einwand verstehe ich nicht.
Ich habe den Aufschlagpunkt bei (0/2,55) angesetzt und bei meiner Funktionsgleichung kommt er (bis auf Rundungsabweichungen) auch raus.
-0,27 * (0-4,3)² + 5 = -0,27 * 4,3² + 5 = -4,99 + 5 = 0,01 (nicht 2,55)
Korrektur!!! Ich habe nochmal auf mein Blatt geguckt, das steht tatsächlich 18,45 a +5 =0 ..... wie doof
Korrektur!!!
Nach der bemerkung von Rhenane stimme ich dir zu
f(x )= -0,13(x-4,3)²+5
hatte ich auch zuerst für a - weil ich (wie Du wohl auch), y=0 statt 2,55 angesetzt habe!