Extremwertaufgabe Randwerte?
Guten Tag!
Ich wollte Mal nachfragen um sicher zu gehen und zwar müsste ganz unten bei den Randwerten s‘(n) gegen minus unendlich gehen?
Weil da steht ja auch , dass s vor dem Tiefpunkt monoton fallend ist.
Außerdem kriege ich immer kleinere Zahlen raus, wenn ich kleinere Werte(n—>0) in s‘(n) einsetze.
Auch wenn ich den Graph von s‘(n) plotte geht der Graph gegen minus Unendlich für n—>0.

3 Antworten
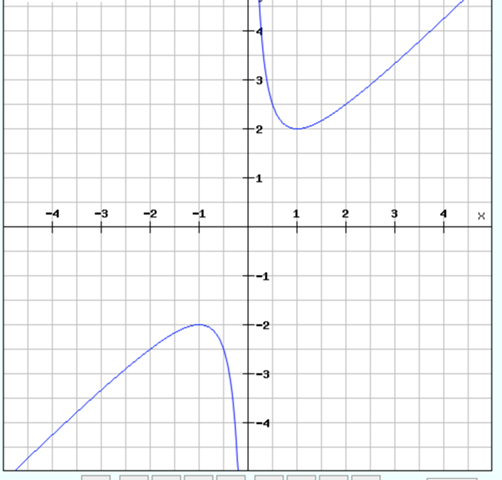
So sieht der Graph aus:

Der linke Zweig interessiert uns nicht, da n positiv sein muss.
In der Tat liegt bei n = 1 ein globales Minimum innerhalb des Defintionsbereiches.
Weil da steht ja auch , dass s vor dem Tiefpunkt monoton fallend ist.
Stimmt, denn man betrachtet den Graphen immer von links nach rechts und von 0 bis 1 ist er monoton fallend.
Außerdem kriege ich immer kleinere Zahlen raus, wenn ich kleinere Werte(n—>0) in s‘(n) einsetze.
s' gibt die Steigung an. Die interessiert hier aber nicht, sondern es interessieren die Funktionswerte s(n). Dass s' immer kleiner wird und zwischn 0 und 1 sogar negativ ist, sieht man am Graphen. Links von 1 ist die Steigung negativ. Aber wie gesagt, das ist hier nicht die Frage.
Auch wenn ich den Graph von s‘(n) plotte
Wozu plottest du s' und nicht s?

Aus dem Plot von s' kannst du lediglich entnehmen, dass sich bei +1 und -1 Extrema befinden und aus der positiven Steigung bei +1 kannst du entnehmen, dass das ein Tiefpunkt ist und aus der negativen Steigung bei -1 kannst du entnehmen, dass sich bei -1 ein Hochpunkt befindet, denn die Steigung von s' ist ja = s' '
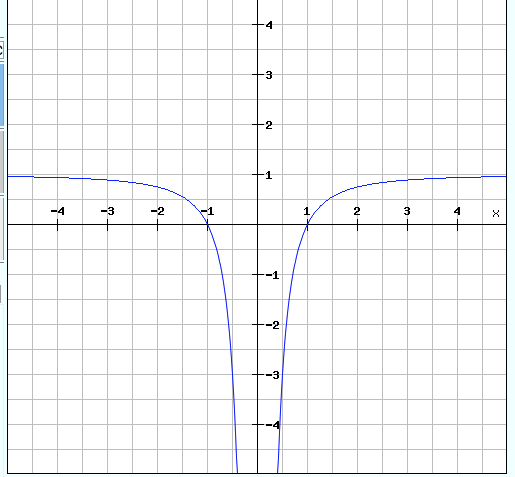
Also könnte man sich das prüfen des Monotonieverhaltens mit s‘ sparen
Ja, das macht keinen Sinn im Hinblick auf die Aufgabe.
zwar müsste ganz unten bei den Randwerten s‘(n) gegen minus unendlich gehen?
Korrekt.
Anmerkung: Warum jemand auch noch die Stelle n = -1 untersucht, erschließt sich mir nicht, da n ∈ ℕ sein soll.
Das mit n habe ich mich auch gefragt !
Irgendwie wurde bei jeder dieser Extremwert Aufgaben, Werte überprüft die garnicht im Df Bereich sind.
Danke!!
für n gegen Null , egal von welcher Seite aus , ist limes MINUS Unendlich
schnell kann mal ein Minus vergessen werden in einer Lösungsangabe
Vielen vielen Dank! :)
Also könnte man sich das prüfen des Monotonieverhaltens mit s‘ sparen und einfach bei s(n) die Funktionswerte für n—>0 und n—> unendlich untersuchen?
Denn dann geht ja Für n—>0 s(n) gegen unendlich
und für n—> unendlich s(n) auch gegen unendlich .
Somit ist auch bei n=1 das globale Minimum.