Extremalproblem BITTE ERKLÄREN?

Hallo,

ich habe momentan Extremalprobleme, mit Betonung auf Problem… Habe keine Probleme bei den etwas einfacheren gehabt aber muss jetzt gefühlt für jede einzelne Aufgabe hier nachfragen. Könnte jemand sich die Zeit nehmen und Schritt für Schritt anhand meiner Aufgabe erklären wie er/sie vorgeht. Ich verzweifele echt dran, bekomme bei etwas schwierigeren Aufgaben nichts von alleine auf die Reihe… Vielen Dank wenn sich jemand die Zeit nimmt 🙏🏼

Answer 1

[mihisu]

Zunächst solltest du schauen, welche Größe maximal/minimal werden soll, und wie man diese in dem Zusammenhang berechnen könnte.

Im konkreten Fall soll die Tragfähigkeit T maximal werden. Und für diese Tragfähigkeit ist auch bereits eine Formel angegeben:

$T=b\cdot h^2$

[Hinweis: Solch eine Funktionsgleichung, welche die zu optimierende Größe (hier: T) in Abhängigkeit von anderen größen beschreibt, nennt man auch „Zielfunktion“.]

Ohne weitere Informationen könnte die Tragfähigkeit T beliebig groß werden (theoretisch unendlich groß), wenn man b und h entsprechend groß wählt. Aber: Man kann b und h nicht beliebig groß wählen. Wie es auch bei anderen Extremalproblemen oft der Fall ist, hat man noch Nebenbedingungen, die eingehalten werden müssen. Im konkreten Fall soll der Balken „aus einem Rundholz mit dem Durchmesser 30 cm geschnitten werden“.

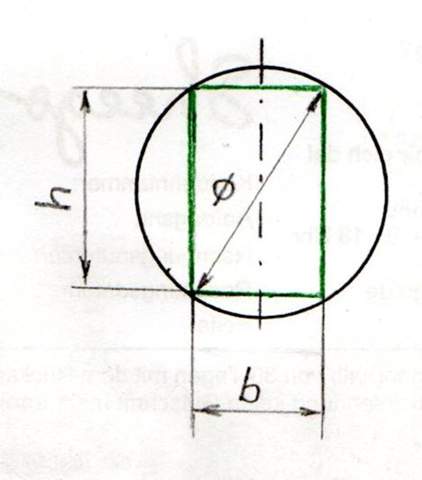
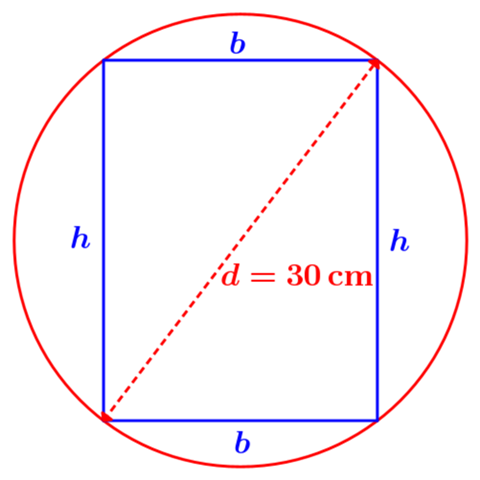
Nun hilft eine Skizze, um das zu veranschaulichen, wenn man sich das nicht schon entsprechend im Kopf vorstellen kann. Wenn man den kreisförmigen Querschnitt eines entsprechenden Runholzes und beispielhaft einen entsprechenden Querschnitt des daraus geschnittenen Balkens skizziert, kann das beispielsweise so aussehen...

[Vorausgesetzt habe ich dabei, man macht den Balken so groß, dass er bis zum Rand des Rundholzes reicht. (Man könnte den Balken natürlich auch kleiner machen, aber dann würde das Rundholz offensichtlich nicht optimal ausgenutzt werden. Das würde dann zu b² + h² ≤ d² statt b² + h² = d², was die Rechnung nur unnötig kompliziert machen würde, und letztendlich dann doch das gleiche Ergebnis liefern würde.)]

Ein eingezeichneter Durchmesser des Rundholzes teilt den rechteckigen Balkenquerschnitt in zwei rechtwinklige Dreiecke auf. Mit Hilfe des Satzes des Pythagoras erhält man bei einem solchen rechtwinkligen Dreieck dann...

$b^2+h^2=d^2\quad \left(\text{mit }d=30\,\text{cm}\right)$

Diese Nebenbedingung kann man nun nutzen, um zu erreichen, dass die Zielfunktion von nur noch einer unbekannten Größe abhängt.

Wenn man die Nebenbedingung beispielsweise nach h² auflöst und dann das h² in der Zielfunktion entsprechend ersetzt, hängt die Zielfunktion nur noch von einer unbekannten Größe (hier dann: b) ab.

$b^2+h^2=d^2\quad \rightarrow\quad h^2=d^2-b^2$

$\rightarrow\quad T=b\cdot \overbrace{\left(d^2-b^2\right)}^{h^2}$

$\rightarrow\quad T=d^2\cdot b-b^3$

Nun so hat man eine Funktionsgleichung, bei der T nur noch von einer unbekannten Größe b abhängt. [Nur falls du dich wunderst: d ist hier keine unbekannte Größe, da man ja konkret d = 30 cm gegeben hat. Das habe ich hier nur gerade noch nicht eingesetzt.]

Nun kann man mit analytischen Mitteln das Maximum dieser Funktion finden. [Schauen, wo die Ableitung ihr Vorzeichen von positiv zu negativ wechselt. Bzw. alternativ, wo die Ableitung 0 wird und die zweite Ableitung negativ ist.]

$T(b)=d^2\cdot b-b^3\quad \rightarrow\quad T'(b)=d^2-3\cdot b^2$

$T'(b)=0\quad \Leftrightarrow\quad d^2-3\cdot b^2=0$

$\quad \Leftrightarrow\quad 3\cdot b^2=d^2$

$\quad \Leftrightarrow\quad b^2=\frac{d^2}{3}$

$\quad \xLeftrightarrow{b>0}\quad b=\sqrt{\frac{d^2}{3}}$

$\quad \Leftrightarrow\quad b=\frac{\sqrt{d^2}}{\sqrt{3}}$

$\quad \xLeftrightarrow{d>0}\quad b=\frac{d}{\sqrt{3}}$

Damit hat man dann die Breite des Balkens gefunden...

$b=\frac{d}{\sqrt{3}}=\frac{30\,\text{cm}}{\sqrt{3}}\approx 17\text{,}32\,\text{cm}$

Wenn man die Gleichung h² = d² - b² aus der Nebenbedingung weiter nach h auflöst und die soeben erhaltene Balkenbreite einsetzt, erhält man die Höhe des Balkens...

$h=\sqrt{d^2-b^2}\approx \sqrt{\left(30\,\text{cm}\right)^2-\left(17\text{,}32\,\text{cm}\right)^2}\approx 24\text{,}49\,\text{cm}$

Ergebnis: Die optimalen Maße des Balkens betragen b ≈ 17,32 cm und h ≈ 24,49 cm.

============

Zusammenfassend sind die wesentlichen Schritte, die so auch bei vielen ähnlichen Extremalproblemen so auftreten...

1. Zielfunktion finden (Also: Die zu optimierende Größe in Abhängigkeit anderer Größen darstellen)
2. Nebenbedingungen finden (Also: Was gibt es noch für Einschränkungen der unbekannten Größen, von denen die Zielfunktion abhängt? Dazu hilft vielleicht eine Skizze.)
3. Gleichungen aus den Nebenbedingungen nach einer unbekannten Größe auflösen und in die Zielfunktion einsetzen. (Ziel: Anzahl der unbekannten Größen in der Zielfunktion reduzieren)
4. Wenn die Zielfunktion nur noch von einer unbekannten Größe abhängt: Das entsprechende Maximum bzw. Minimum mit Hilfe analytischer Mittel (insbesondere mit Hilfe der ersten Ableitung) finden, und für welchen Wert der unbekannten Größe dieses Maximum/Minimum auftritt.
5. Gegebenenfalls die Werte der anderen unbekannten Größen dann mit Hilfe der bisher berechneten Werte berechnen, indem man die bereits berechneten Werte in die in Schritt 3 aufgelösten Gleichungen der Nebenbedingungen einsetzt.
6. Antwort formulieren, in der die Ergebnisse genannt werden.

Answer 2

[Halswirbelstrom]

LG H.