Was ist die Lösung?

Mit Rechenweg bitte!

Answer 1

[mihisu]

Berechne den Flächeninhalt der gelben Fläche und multipliziere diesen Flächeninhalt mit der Länge 1 m des Kanalsegments.

Die gelbe Fläche kann man beispielsweise folgendermaßen in drei Teilflächenzerlegen, die ich in der folgenden Skizze blau bzw. rot markiert habe.

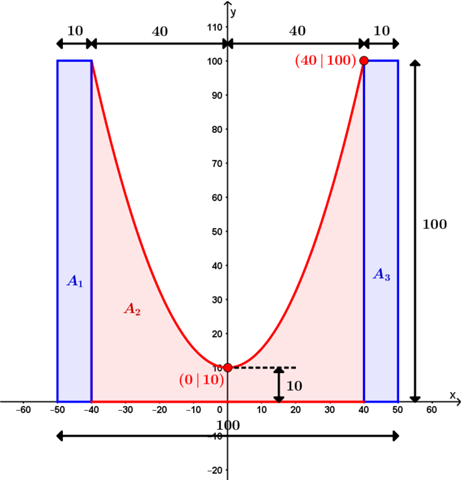
Da habe ich auch gleich ein Koordinatensystem für die Parabel reingelegt.

Für den Flächeninhalt eines der beiden blauen Rechtecke [Längen in cm; Flächeninhalte in cm²] erhält man offensichtlich...

$A_1=A_3=10\cdot 100=1000$

Die Parabel geht von x = -40 bis x = 40. Auf die 40er-Werte kommt man, indem man von der Gesamtbreite 100 die Breiten der beiden blauen Rechtecke subtrahiert [100 - 10 - 10 = 80] und diese Länge dann halbiert.

Die Parabel hat (so wie ich das Koordinatensystem gelegt habe) ihren Scheitelpunkt bei (0 | 10). Dementsprechend erhält man als Ansatz für eine entsprechende Funktionsgleichung:

$f(x)=a\cdot x^2+10$

Nun muss beispielsweise noch der Punkt (40 | 100) enthalten sein...

$f(40)=100\quad \Leftrightarrow\quad a\cdot 40^2 +10=100$ $\Leftrightarrow\quad a\cdot 40^2 =90$ $\Leftrightarrow\quad a=\frac{90}{40^2}$ $\Leftrightarrow\quad a=\frac{9}{160}$

Dementsprechend erhält man als Funktionsgleichung:

$f(x)=\frac{9}{160}\,x^2+10$

Für Flächeninhalt der rot in meiner Skizze markierten Fläche erhält man dann mittels Integralrechnung...

$A_2=\int\limits_{-40}^{40}f(x)\,\text{d}x$

$=\int\limits_{-40}^{40}\left(\frac{9}{160}\,x^2+10\right)\,\text{d}x$

$=\left[\frac{9}{160}\cdot \frac{1}{3}\,x^3+10\cdot x\right]_{-40}^{40}$

$=\left[\frac{3}{160}\,x^3+10\, x\right]_{-40}^{40}$

$=\left(\frac{3}{160}\cdot {40}^3+10\cdot 40\right)-\left(\frac{3}{160}\cdot {\left(-40\right)}^3+10\cdot \left(-40\right)\right)$

$=3200$

Insgesamt erhält man dann für die gesamte (in der Aufgabenstellung gelb markierte) Fläche...

$A_1+A_2+A_3=1000+3200+1000=5200$

Der Flächeninhalt der gelben Fläche beträgt dementsprechend 5200 cm².

Für das gesuchte Volumen muss man jetzt noch mit 1 m (= 100 cm) multiplizieren.

Ergebnis:

$5200\,\text{cm}^2\cdot 100\,\text{cm}=520000\,\text{cm}^3=520\,\text{dm}^3=0\text{,}52\,\text{m}^3$

Answer 2

[evtldocha]

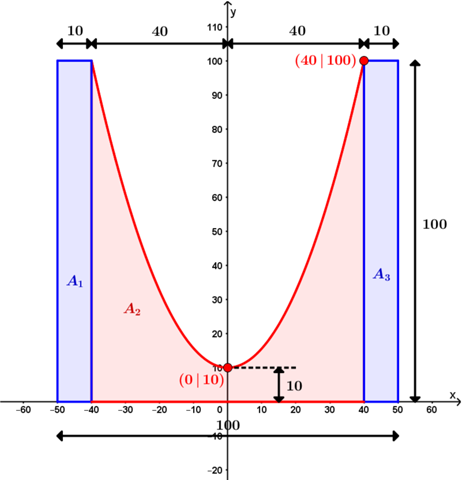
Berechne den Querschnitt (in cm² !!!) zu:

$Q=100^2-\int_{_{-40}}^{^{40}}\left(\frac{9}{160}x^2+10\right)dx$

Hinweis:

Die Parabelgleichung p(x) ergibt sich aus dem Scheitelpunkt zu $p\left(x\right)=a\cdot x^2+10\$

und der Bedingung $p\left(40\right)=100\ \rightarrow\ a\cdot1600\ +\ 10\ =\ 100\ \rightarrow\ a=\frac{90}{1600}=\frac{9}{160}$

Das Volumen ergibt sich dann zu (siehe das unterstrichene meter in meterweise)

$V=Q\cdot1m\$