Warum ist Cos(×)+1 achsensymmetrisch?

Hallo zusammen, ich soll die Funktion cos(x)+1 auf Symmetrie untersuchen. In den Lösungen stand sie sei achsensymmetrsich zur y-Achse. Das verwirrt mich aber, weil wenn die Hochzahlen ungerade sind prüft man doch auf Punktsymmetrie und cos(×) hat doch eine ungerade Hochzahl nämlich 1? Warum ist das dann achsensymmetrisch?

Hier habe ich dann auf Achsensymmetrie geprüft, aber das ist doch nicht das selbe oder?

Answer 1

[Applwind]

Hier der Nachweis, wahrscheinlich nicht verständlich, aber es stimmt. Die Funktion f(x) = cos(x) ist eine gerade Funktion und + 1, wegen 1*x^0 und 0 € 2IN auch.

Answer 2

[ShimaG]

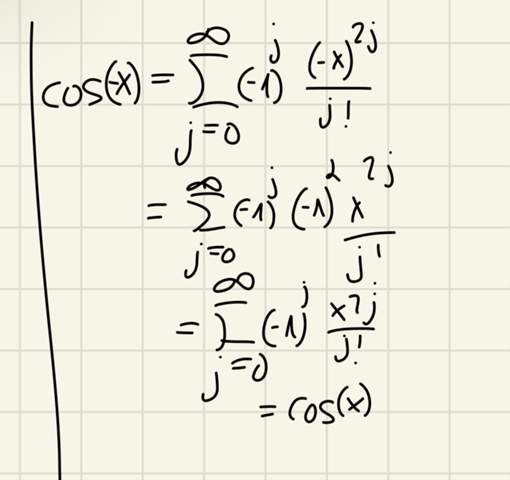
Es geht um die Exponenten von x. Da 1 = 1 * x^0 hat die Konstanten 1 (und jede Konstante) einen geraden Exponenten, nämlich Null.

Die Taylorreihe des Cosinus hat nur gerade Exponenten und ist damit achsensymmetrisch.

Answer 3

[W00dp3ckr]

Schau Dir die Taylorreihe des Kosinus an. Da sind lauter gerade Exponenten, die anderen sind null. Daher ist das symmetrisch.

Answer 4

[DieChemikerin]

Hi,

deine Symmetrieregeln gelten für Polynomfunktionen. Das können wir hier auch anwenden. Hier ist es sinnvoll, sich die Taylorreihe der Cosinusfunktion anzusehen: $\cos\left(x\right)=\sum_{n=0}^∞\left(-1\right)^n\cdot\frac{x^{2n}}{\left(2n\right)!}$ $=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}\pm...$

Du siehst: Es sind nur gerade Exponenten. Somit gilt Achsensymmetrie.

LG

Woher ich das weiß: Hobby – seit der Schulzeit, ehemals Mathe LK