Mathe hilfe Zahl zerlegen?
Hallo Freunde,
die Aufgabe 1 lautet wie folgt:
Ermitteln Sie eine Zerlegung der Zahl 12 in zwei nicht-negative Summanden, so dass die Summe ihrer Quadrate möglichst groß wird.
mein ansatz ist f(x)=x²+(12-x)²
1 Antwort
dagegen ist nix zu sagen :))
Summand 1 ist x , Summand 2 ist dann 12-x . Beides im Quadrat und als Summe geschrieben
Als f(x) eine Parabel und sieht so aus
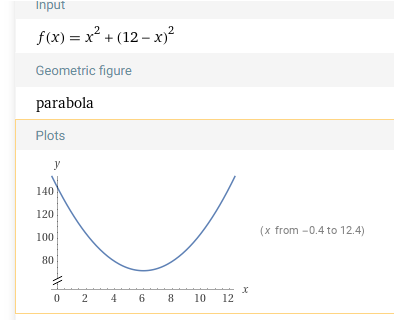
da fällt einem aber auf ( mir auch gerade ), dass es nur ein Min , aber kein Max gibt
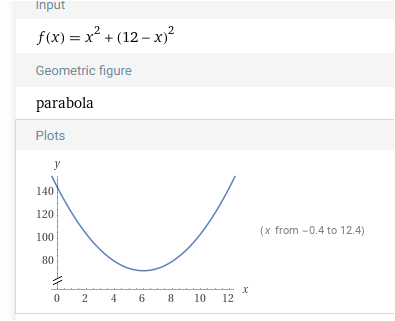
Die Extreme liegen also auf den Randpunkten des Intervalls.
du musst das globale Max im Bereich 0 bis 12 bestimmen ( wenn die 0 bei dir als nicht negative Zahl betrachtet wird )
ist mir auch grad aufgefallen . Voraussetzung : Die 0 darf als nichtnegative Zahl gewertet werden . Sonst gibt es ja gar kein Max, oder ?
Die Formulierung "nicht-negative Zahl" ist offensichtlich genau darauf abgestimmt. Negative Zahlen sind kleiner als Null.
wenn du schon Integrale kennst , musst du Ableiten schon lange gelernt haben.
Sonst hilft nur Probieren . Du bist also in der siebenten Klasse ?
dann ist alles Schwierig : Hier musst du feststellen , dass kein relatives Max vorliegt und du daher den größten y-Wert im gesamten Intervall suchen musst ( das sogenannte globale Maximum )
Und der liegt bei x = oder bei x = 12
was in beiden fällen zu 144 als Summe der Quadrate führt.
Aber wie geht es weiter nach dem ansatz?