[Mathe] Hilfe benötigt bei der Bestimmung der Tangenten?
Guten Tag,
ich benötige noch ein wenig Hilfe bei der Aufgabe b).
Meine Ansatz zur Aufgabe b):
Ich sehe direkt, dass es drei Tangenten an Kg gibt, welche durch den Punkt P(0/1) verkaufen. Einmal eine Tangente bei x = - …, einmal bei x = + … und einmal eine Tangente bei x = 0. Diese Tangente bei x = 0 hat die Gleichung t(x) = 1.
- Nun bin ich mir aber unsicher, was unter „Untersuchen Sie“ gemeint ist. Denn ich habe es ja nur schriftlich und nicht rechnerisch gemacht.
- Was meint ihr, muss ich es auch noch rechnerisch zeigen, dass es wirklich drei Tangente an Kg gibt?
- Könnt ihr mir vielleicht die rechnerische Bestimmung genau erklären?
Im folgenden befindet sich ein Bild der Aufgaben a) und b) (inklusive meiner bearbeiteten Aufgabe a)), wobei sich meine Fragen nur auf die Aufgabe b) beziehen. Zudem befindet sich danach ein Foto des Lösungsvorschlags.
Ich freue mich sehr auf eure ausführlichen und leicht verständlichen Antworten.
[Aufgaben]

[Bearbeitete Aufgabe a)]

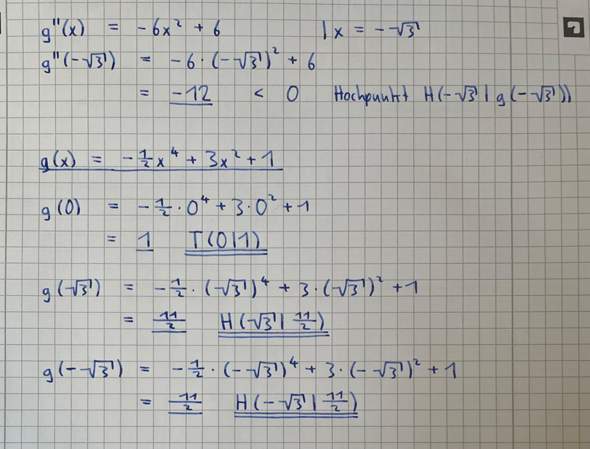
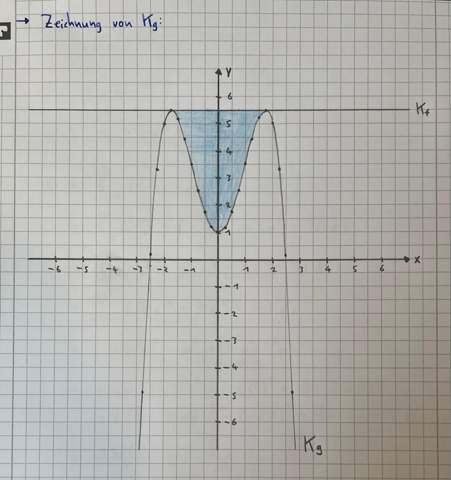
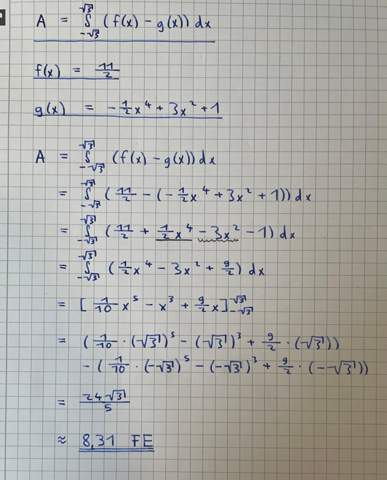
[Lösungsvorschlag]
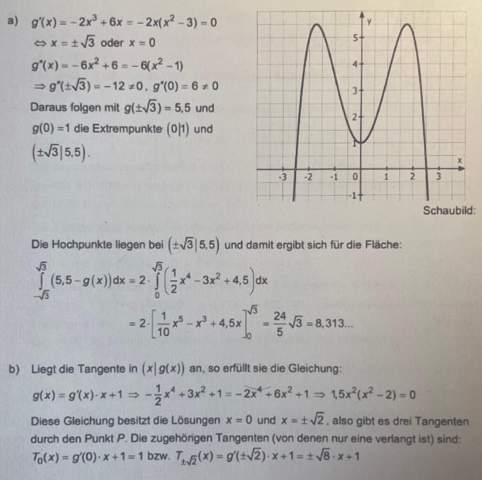
2 Antworten

Nun bin ich mir aber unsicher, was unter „Untersuchen Sie“ gemeint ist.
Es muss auf jeden Fall eine Herleitung mit den Mitteln der Mathematik erfolgen.
"Ich sehe sofort..." würde ich nicht dazu zählen, obwohl es tatsächlich offensichtlich ist. So bleibt entweder eine rechnerische oder eine graphische Herleitung.
Bei der graphischen Herleitung könnte man so vorgehen:
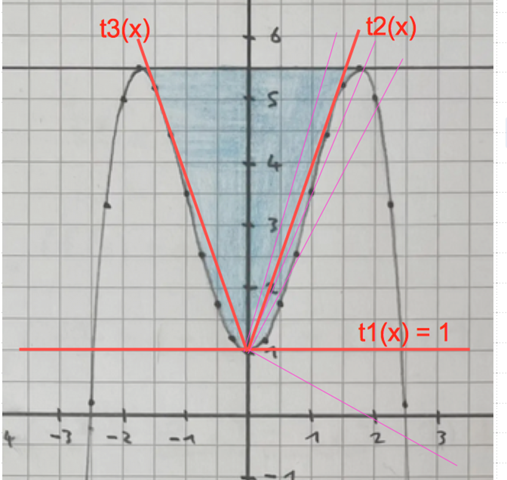
Es gibt nur 3 Möglichkeiten, eine Tangente einzuzeichnen, die sowohl durch A(0/1) geht als auch den Graphen von g(x) berührt und nicht echt schneidet, siehe Skizze:
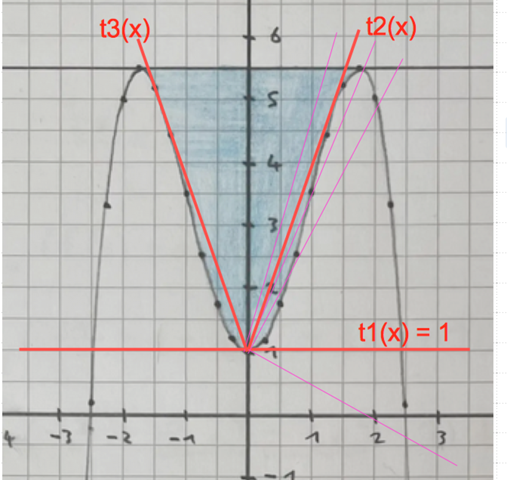
Was meint ihr, muss ich es auch noch rechnerisch zeigen, dass es wirklich drei Tangente an Kg gibt?
Ich fürchte ja. Als Korrektor würde ich aber auch die graphische Untersuchung gelten lassen.
Könnt ihr mir vielleicht die rechnerische Bestimmung genau erklären?
Ansatz der Tangentengleichung:
t(x) = mx + 1
Für die Tangente gilt im Berührpunkt:
m = g'(x)
daraus folgt für den Berührpunkt:
t(x) = g'(x) * x + 1 = (-2x^3 + 6x)x + 1
t(x) = -2x^4 + 6x^2 + 1
Der Berührpunkt muss sowohl auf der Tangente als auch auf dem Graphen von g(x) liegen. Daher schneiden wir die beiden durch Gleichsetzen:
t(x) = g(x)
-2x^4 + 6x^2 + 1 = -0,5 x^4 + 3x^2 + 1
und lösen nach x auf.
(Korrekterweise müsste man ergänzen und hier hat die Musterlösung einen Mangel):
Ein Berührpunkt liegt für alle doppelten Schnittpunkte vor. Daher können nur doppelte Lösungen der Gleichung einen Berührpunkt ergeben. Einfache Lösungen ergeben echte Schnittpunkte mit Durchdringung der beiden Graphen.
Auflösen nach x:
-2x^4 + 6x^2 + 1 = -0,5 x^4 + 3x^2 + 1 ∣ -1
-2x^4 + 6x^2 = -0,5 x^4 + 3x^2 ∣ + 0,5x^4
-1,5x^4 + 6x^2 = 3x^2 ∣ - 3x^2
-1,5x^4 + 3x^2 = 0
x^2 (3 - 1,5x^2) = 0
erste doppelte Nullstelle bei x = 0
zugehörige Tangentengleichung:
m = g'(0) = 0
t(x) = 0*x + 1
t(x) = 1
Weitere Nullstellen:
3 - 1,5x^2 = 0
1,5 x^2 = 3
x^2 = 3/1,5 = 2
Auch hier handelt es sich wegen des Quadrates um eine doppelte Nullstelle, womit ein Berührpunkt vorliegt:
x = ±√2
Lösung: es gibt mögliche 3 Berührpunkte und damit 3 mögliche Tangenten. Eine davon hat die Gleichung:
t(x) = 1

Wow! Einfach nur wow! Sehr hilfreich 🤩 Vielen lieben Dank :-) Hättest du solche Lösungsvorschläge verfasst, hättest du hier fast keine einzige Frage von mir.

Vielleicht magst du dir ja noch eine weitere Frage von mir ansehen, bei der ich leider noch nicht verstehe, wie man die Eigenschaften der gegebenen Bedingungen erklären kann: https://www.gutefrage.net/frage/mathe-eigenschaften-der-gegebenen-bedingungen-nennen 🙋♂️ :-)

Du hast Recht. Ich ziehe mein Argument in diesem Fall mit der doppelten Nullstelle zurück. Die Eigenschaft des Berührpunktes wurde ja bereits mit der Bedingung
m = g'(x)
daraus folgt für den Berührpunkt:
t(x) = g'(x) * x + 1 = (-2x^3 + 6x)x + 1
t(x) = -2x^4 + 6x^2 + 1
ausreichend "eingepreist".

Vielen lieben Dank für deine Rückmeldung.
Nehmen wir mal an, du möchtest dennoch nur die doppelten Nullstellen berechnen, dann ist das aber doch keine doppelte Nullstelle, wie du sagtest:
Auch hier handelt es sich wegen des Quadrates um eine doppelte Nullstelle, womit ein Berührpunkt vorliegt:
x = ±√2
Da habe ich ja ein Beispiel dazu in meinem Kommentar hier genannt.


Okay, dann sind das einfache Nullstellen, wenn man eine Wurzel zieht und zwei verschiedene Ergebnisse erhält. Das hatte mich nämlich echt ein bisschen verwirrt.

f(x) = -1/2*x⁴ + 3*x² + 1
Die allgemeine Tangentengleichung am Punkt a lautet
t(x) = f'(a)*(x-a) + f(a)
t(x) = (-2*a³ + 6*a)*(x-a) + -1/2*a⁴ +3*a² + 1
Für mögliche Tangenten muss gelten:
t(0) = 1
t(0) = (-2*a³ + 6*a)*(-a) + -1/2*a⁴ +3*a² + 1
t(0) = 3/2*a⁴ - 3a² + 1
Daraus folgt:
3/2*a⁴ - 3a² + 1 = 1
3/2*a⁴ - 3a² = 0
Das gilt für:
a = 0
a = -sqrt(2)
a = +sqrt(2)
Warum handelt es sich auch um einen Berührpunkt, wenn man bei x^2 zwei verschiedene Werte für x erhält? Bis jetzt kannte ich es nur, dass es sich um einen Berührpunkt handelt, wenn man ein einziges Ergebnis erhält, wenn man x^2 auflöst. Beispiel: x^2 = 0 -> x1/2 = 0 (doppelte Nullstelle / Berührpunkt). Beim Auflösen von x^2 = 2 erhält man ja x1 = +Wurzel2 und x2 = -Wurzel2. Hierbei bin ich immer davon ausgegangen, dass es sich um einfache Nullstellen handelt.
Hierfür habe ich mir ein Beispiel in Form einer Funktion ausgedacht, um dir genau zu zeigen, was ich nicht so ganz verstehe (den Teil in deiner Antwort oben: „Auch hier handelt es sich wegen des Quadrates um eine doppelte Nullstelle, womit ein Berührpunkt vorliegt.“):
f(x) = x^2 (x^2 - 2)
x^2 = 0
x1/2 = 0 (doppelte Nullstelle / das Schaubild von Kf berührt die x-Achse bei x = 0)
x^2 - 2 = 0
x^2 = 2
x3 = +Wurzel2 (einfache Nullstelle / das Schaubild von Kf schneidet die x-Achse bei x = +Wurzel2)
x4 = -Wurzel2 (einfache Nullstelle / das Schaubild von Kf schneidet die x-Achse bei x = -Wurzel2)