Mathe Hausaufgabe?
Gymnasium 11. Klasse (G9). Wir haben heute das Thema Stetigkeit eingeführt. Ich verstehe wirklich gefühlt kein Wort in Mathe und sitze seit einer Stunde an dieser (laut unserem Lehrer) „einfachen“ Aufgabe. Sind nicht alle drei nicht stetig? Woran sieht man es hier genau? Bitte Hilfe und wenn möglich eine Erklärung 😭✨

VG Shadow
4 Antworten
Sind nicht alle drei nicht stetig?
Achtung: Der Begriff Stetigkeit ist zuerst mal keine globale Aussage über die Funktion, sondern bezieht sich auf bestimmte Punkte oder Intervalle. Die Aussage wäre dann etwa: Die Funktion in c) ist überall stetig außer in x = 0 und x = 1. Daher steht in der Aufgabe auch die Formulierung, dass Du die Stetigkeit an den Nahtstellen (das sind die "bestimmten Punkte") prüfen sollst.
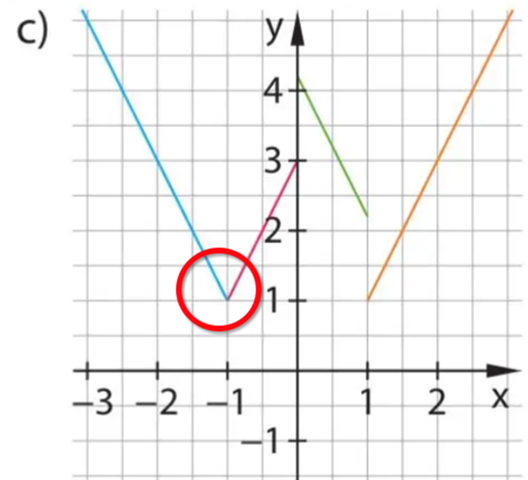
Nur an der mit einem roten Kreis gekennzeichnete Schnittstelle ist die Funktion in Aufgabe c) stetig (rechtsseitiger Grenzwert = linksseitiger Grenzwert bei x=-1 ist jeweils identisch = 1). Bei allen anderen "Nahtstellen" sehe ich einen Sprung

Woran sieht man es hier genau?
An den Sprüngen von z.B. grün y= ~2,25 auf gelb y = 1 bei x=1. Daher ist die Funktion bei x = 1 nicht stetig.
Ich sehe auch einen Sprung ! Also kein Grund für dich , den Fielmann deiner Wahl aufzusuchen
Sagte nicht auch Loriot schon : Ja , wo springen sie denn ?
Grundsätzlich bedeutet Stetigkeit, dass sich bei geringfügiger Änderung des x-Werts (also wenn du von einem bestimmten x-Wert ein kleines bisschen nach links oder rechts zu einem anderen x-Wert gehst, der in der Nähe liegt und nur wenig größer oder kleiner ist als der bisherige) auch die zugehörigen Funktionswerte nur wenig verändern. Das ist wie, schon von jemand Anderem erwähnt, vereinfacht gesagt immer dann der Fall, wenn du deine Funktion an einem Stück durchzeichnen kannst, ohne deinen Stift absetzen zu müssen, du also keine Sprungstellen hast.
Hast du an bestimmten Stellen (wie in der 1. Funktion bei x=1) Sprungstellen, dann siehst du, dass dort (also bei x=1) eine geringfügige Änderung des x-Werts nach rechts zu einer deutlich größeren Änderung der y-Werte führt (da du von der einen zur anderen Teilfunktion springen musst). Wenn du im Gegensatz dazu die gleiche Änderung nur auf der linken bzw. nur der rechten Teilfunktion machen würdest, würden sich auch die Funktionswerte nur wenig verändern, da die beiden Teilfunktionen da jeweils stetig sind.
Die Nahtstellen sind interessant.
Schau Dir diese Defintion an:
Eine Funktion x → f(x) heißt an der Stelle x = x₀ stetig, falls
1) x₀ ϵ D
2) lim (x → x₀+) f(x) = lim (x → x₀-) f(x)
3) lim (x → x₀) f(x) = f(x₀)
In diesem Sinne ist ein "Knick" zulässig, ein "Sprung" aber nicht.
etwas "unmathematisch": eine Funktion ist stetig, wenn Du deren Graphen innerhalb des Definitionsbereichs zeichnen kannst, ohne den Stift abzusetzen. D. h. bei Dir ist nur die Funktion bei c) an der Nahtstelle x=-1 stetig, an allen anderen Nahtstellen machen die Graphen Sprünge.
a) ist an der Stelle x = 1 nicht stetig. Da liegt ein Sprung vor. Wenn man sich dieser Stelle von rechts nähert, erhält man einen anderen Funktionswert, als wenn man sich von der linken Seite nähert.
wenn ihr noch nicht "so weit" seid, dann reicht wahrscheinlich die Begründung
Sprung : Nicht
Kein Sprung : Stetig
.
Deswegen ist die Aufgabe dann tatsächlich "einfach"
.
Lehrerinnen sollten sehr vorsichtig mit dem Begriff "einfach"
Auch wenn ich etwas erkläre kann er mir schon mal rausrutschen . Ist aber VOLL DOOF
So weit waren wir im Unterricht noch gar nicht haha. Aber das bedeutet jetzt das a) stetig ist, oder nicht? Sorry, ich kann echt kein Mathe.