Mathe extremwertprobleme?
Ich hänge leider wider an einer Aufgabe die ziemlich schwer ist, also ich hab schon einen Ansatz dafür entwickelt aber ich komme nicht weiter, ich glaube die aufgabe ist echt viel zu schwer. Es könnte sein dass es wahrscheinlich einfacher wäre zuerst allgemein zu rechnen also mit s und dann lieber s am ende einfach einzusetzen . Also zuerst b zu lösen und dann die Aufgabe a…
danke im voraus


V abzuleiten ist echt unmöglich gewesen deswegen habe ich es bei chatgpt eingegeben,aber ohne hätte ich es nicht geschafft trotzdem komme ich leider nicht weiter
4 Antworten
Die gehen doch alle gleich: Du schreibst einfach die Volumsformel V=⅓r²πh als Funktion von r oder h an und bestimmst das Minimum. Da s gegeben ist, kannst Du den Πυθαγόρας heranziehen, weil s²=r²+h² (die Höhe steht ja normal auf die Grundfläche), und es empfiehlt sich, das Volumen als Funktion von h zu wählen, weil man dann das r² ohne Wurzel durch h ausdrücken kann.

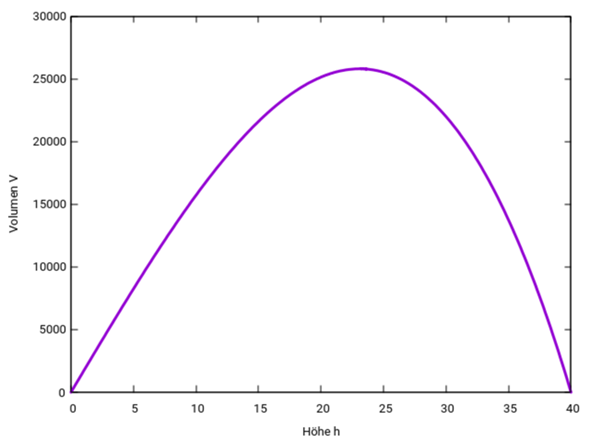
Und jetzt brauchst Du nur noch s²−3h²=0 nullzusetzen und erhältst h=√(⅓s²)=√⅓⋅s≈23.1 und für r=√(s²−h²)=√⅔⋅s≈32.7. Das Volumen beträgt dann V=⅓r²πh≈25796.

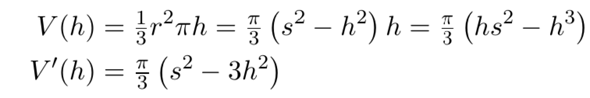
Extremalbedingung:
V_Kegel = (1/3) * r² * π * h → Maximum
Nebenbedingung:
s² = h² + r²
Nebenbedingung nach r oder h umstellen und in die Extremalbedingung einsetzen. Ableiten, gleich Null setzen und Maximum bestimmen, ...
Wenn man in der Extremalbedingung r² durch s² - h² ersetzt, wird es überschaubar.
Wenn du b gemacht hast, ist es zwar einfach a zu machen, da hast du Recht. Aber ich finde es trotzdem einfacher, erst a zu machen, weil man sich mit Zahlen üblicherweise einfach leichter tut. Für b kannst du dann einfach nachsehen, wie du bei a gerechnet hast und das in einer Formel packen. Aber mach einfach, wie du dir leichter tust...
Substituiere r² statt h → dann hast du keine Wurzel, die Ableitung wird einfacher.
Ja aber es ist nicht so einfach wie es klingt , die formel ist echt kompliziert