Kann jemand bitte die Stetigkeit und differnzierbarkeit berechnen als Beispiel für mich?

Answer 1

[mihisu]

Bei der Stetigkeit sind hier vor allem die Übergangsstellen bei x = -1 und bei x = 2 relevant. Denn an den anderen Stellen kann man nutzen...

Wenn man stetige Funktionen miteinander verknüpft [d.h. Summen, Differenzen, Produkte, Quotienten (natürlich nur dort, wo nicht durch 0 dividiert wird), Verkettungen von stetigen Funktionen], erhält man wieder eine stetige Funktion.

Also kann man zunächst einmal schreiben...

An den Stellen x₀ mit x ₀ < -1 bzw. mit -1 < x₀ < 2 bzw. mit x₀ > 2 ist die Funktion f stetig. Da die Funktion dort jeweils in einer Umgebung um x₀ mit einer offensichtlich stetigen Funktion (da Summen, Differenzen, Produkte, Quotienten stetiger Funktionen stetig sind) übereinstimmt.

Das Gleiche gilt für die Differenzierbarkeit...

An den Stellen x₀ mit x₀ < -1 bzw. mit -1 < x₀ < 2 bzw. mit x₀ > 2 ist die Funktion f differenzierbar. Da die Funktion dort jeweils in einer Umgebung um x₀ mit einer offensichtlich differenzierbaren Funktion (da Summen, Differenzen, Produkte, Quotienten differenzierbarer Funktionen differenzierbar sind) übereinstimmt.

============

Für die Stetigkeit an der Stelle x₀ muss überprüft werden, ob der (beidseitige) Grenzwert an dieser Stelle mit dem Funktionswert an dieser Stelle übereinstimmt.

$\lim\limits_{x\to x_0}f(x)=f(x_0)$

Bzw. wenn die einseitigen Grenzwerte existieren und miteinander übereinstimmen, so existiert auch der beidseitige Grenzwert und stimmt mit den einseitigen Grenzwerten überein. Dementsprechend kann man das auch als...

$\lim\limits_{x\nearrow x_0}f(x)=\lim\limits_{x\searrow x_0}f(x)=f(x_0)$

... formulieren.

Jedenfalls ist im konkreten Fall an der Stelle x₀ = -1 dann für den linksseitigen Grenzwert der Term für x ≤ -1 relevant, für den rechtsseitigen Grenzwert der Term für -1 < x ≤ 2 relevant und für den Funktionswert der Term für x ≤ -1 relevant. Also...

$\lim\limits_{x\nearrow -1}f(x)=\lim\limits_{x\nearrow -1}\left(\frac{2}{x^3}-3x\right)=\frac{2}{\left(-1\right)^3}-3\cdot \left(-1\right)=-2+3=1$

$\lim\limits_{x\searrow -1}f(x)=\lim\limits_{x\searrow -1}\left(x^3-2x+4\right)=\left(-1\right)^3-2\cdot \left(-1\right)+4=-1+2+4=5$

Da der linksseitige Grenzwert nicht mit dem rechtsseitigen Grenzwert übereinstimmt [also der (beidseitige) Grenzwert nicht existiert], ist die Funktion an der Stelle x₀ = -1 nicht stetig. [Dementsprechend ist f keine stetige Funktion.]

An der Stelle x₀ = 2 erhält man...

$\lim\limits_{x\nearrow 2}f(x)=\lim\limits_{x\nearrow 2}\left(x^3-2x+4\right)=2^3-2\cdot 2+4=8-4+4=8$

$\lim\limits_{x\searrow 2}f(x)=\lim\limits_{x\nearrow 2}\left(-\frac{12}{x}+\frac{3}{2}x^2+x+6\right)=-\frac{12}{2}+\frac{3}{2}\cdot 2^2+2+6=-6+6+2+6=8$

$f(2)=2^3-2\cdot 2+4=8-4+4=8$

Dementsprechend existiert der (beidseitige) Grenzwert und stimmt mit dem Funktionswert überein, sodass die Funktion f an der Stelle x₀ = 2 stetig ist.

------ Ergebnis zur Stetigkeitsüberprüfung ------

• Die Funktion f ist an den Stellen x ∈ ℝ∖{-1} stetig.
• Die Funktion f ist an der Stelle x = -1 nicht stetig.
• f ist nicht stetig.

============

Für die Differenzierbarkeit an der Stelle x₀ muss man überprüfen, ob der Differentialquotient...

$\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\quad \left(\text{bzw.}\ \lim\limits_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}\right)$

... exisitiert. [Dabei ist es egal, ob man mit der „x → x₀“-Version arbeitet oder mit der „h → 0“-Version arbeitet. Die beiden Versionen sind zueinander äquivalent. Viele Schüler tun sich jedoch erfahrungsgemäß mit der „h → 0“-Version etwas einfacher.]

Auch hier kann man die Existenz des (beidseitigen) Grenzwerts auf Existenz und Übereinstimmung der einseitigen Grenzwerte zurückführen...

$\lim\limits_{x\nearrow x_0}\frac{f(x)-f(x_0)}{x-x_0}=\lim\limits_{x\searrow x_0}\frac{f(x)-f(x_0)}{x-x_0}$

$\left(\text{bzw.}\ \lim\limits_{h\nearrow 0}\frac{f(x_0+h)-f(x_0)}{h}=\lim\limits_{h\searrow 0}\frac{f(x_0+h)-f(x_0)}{h}\right)$

Zusätzlich sollte dir jedoch auch bekannt sein, dass Differenzierbarkeit auch Stetigkeit impliziert. Wenn eine Funktion an einer Stelle differenzierbar ist, so ist sie an dieser Stelle auch stetig. Umgekehrt gilt dementsprechend: Wenn eine Funktion an einer Stelle nicht stetig ist, so ist sie an dieser Stelle auch nicht differenzierbar. Also erhält man im konkreten Fall...

f ist an der Stelle x₀ = -1 nicht differenzierbar, da die Funktion dort nicht stetig ist.

Dementsprechend muss man nur noch die Stelle x₀ = 2 überprüfen...

$\lim\limits_{h\nearrow 0}\frac{f(2+h)-f(2)}{h}=\lim\limits_{h\nearrow 0}\frac{\left(2+h\right)^3-2\cdot \left(2+h\right)+4-\left(2^3-2\cdot 2+4\right)}{h}$

$=\lim\limits_{h\nearrow 0}\frac{2^3+3\cdot 2^2\cdot h+3\cdot 2\cdot h^2+h^3-2\cdot 2-2\cdot h+4-\left(8-4+4\right)}{h}$

$=\lim\limits_{h\nearrow 0}\frac{8+12 h+6 h^2+h^3-4-2 h+4-\left(8-4+4\right)}{h}$

$=\lim\limits_{h\nearrow 0}\frac{12 h+6 h^2+h^3-2 h}{h}$

$=\lim\limits_{h\nearrow 0}\frac{10 h+6 h^2+h^3}{h}$

$=\lim\limits_{h\nearrow 0}\left(10+6 h+h^2\right)$

$=10+6\cdot 0+0^2=10$

$\lim\limits_{h\searrow 0}\frac{f(2+h)-f(2)}{h}=\lim\limits_{h\searrow 0}\frac{-\frac{12}{2+h}+\frac{3}{2}\cdot \left(2+h\right)^2+2+h+6-\left(2^3-2\cdot 2+4\right)}{h}$

$=\lim\limits_{h\searrow 0}\frac{-\frac{12+6h-6h}{2+h}+\frac{3}{2}\cdot \left(4+4h+h^2\right)+2+h+6-\left(8-4+4\right)}{h}$

$=\lim\limits_{h\searrow 0}\frac{-\frac{12+6h}{2+h}+\frac{6h}{2+h}+6+6h+\frac{3}{2} h^2+2+h+6-8}{h}$

$=\lim\limits_{h\searrow 0}\frac{-6+\frac{6h}{2+h}+6+6h+\frac{3}{2} h^2+2+h+6-8}{h}$

$=\lim\limits_{h\searrow 0}\frac{\frac{6h}{2+h}+\frac{3}{2} h^2+7h}{h}$

$=\lim\limits_{h\searrow 0}\left(\frac{6}{2+h}+\frac{3}{2} h+7\right)$

$=\frac{6}{2+0}+\frac{3}{2}\cdot 0+7$

$=3+0+7=10$

Da die beiden einseitigen Differentialquotienten existieren und miteinander übereinstimmen, existiert auch der (beidseitige) Differentialquotient, weshalb f an der Stelle x₀ = 2 differenzierbar ist.

------ Ergebnis der Differenzierbarkeitsüberprüfung ------

• Die Funktion f ist an den Stellen x ∈ ℝ∖{-1} differenzierbar.
• Die Funktion f ist an der Stelle x = -1 nicht differenzierbar.
• f ist nicht differenzierbar.

====== Ergänzung ======

Anschaulich am Funktionsgraphen bedeutet das... (auch wenn es dir evtl. für den exakten rechnerischen Weg nicht viel bringt)

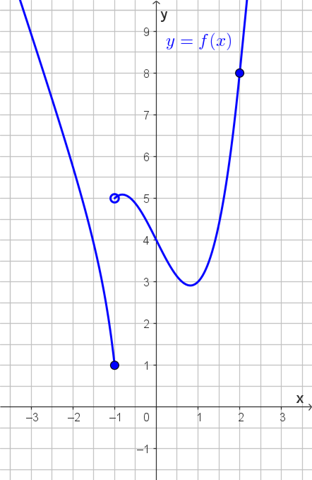
• Die Funktion ist an der Stelle x₀ = -1 nicht stetig, da der linksseitige Funktionswertgrenzwert 1 nicht mit dem rechtsseitigen Funktionswertgrenzwert 5 übereinstimmt. Am Graphen erkennt man an dieser Stelle eine Sprungstelle von y = 1 hoch auf y = 5.
• Die Funktion ist an der Stelle x₀ = -1 auch nicht differenzierbar. Es gibt dort keine definierte Steigung. Die Steigung wäre nämlich an dieser Sprungstelle quasi unendlich groß.
• Die Funktion ist an der Stelle x₀ = 2 stetig. (Grobe Veranschaulichung: Man könnte den Funktionsgraphen in einer Umgebung um die Stelle weiterzeichnen, ohne den Stift abzusetzen.)
• Die Funktion ist an der Stelle x₀ = 2 differenzierbar. Dort hat man keinen Knick oder Ähnliches. Es gibt dort eine eindeutig definierte Steigung (welche übrigens den Wert 10 hat).

Answer 2

[Schachpapa]

Setze die Grenzen der Intervalle, also -1 und 2 für beide Funktionen an der jeweiligen Grenze ein. Wenn jeweils der gleiche Wert herauskommt, ist die Funktion an den entsprechenden Stellen stetig (= hat keine Unterbrechungen / Sprünge).

Setze die Grenzen der Intervalle, also -1 und 2 für beide 1. Ableitungen an der jeweiligen Grenze ein. Wenn jeweils der gleiche Wert herauskommt, ist die Funktion an den entsprechenden Stellen differenzierbar (= hat keine Knicke).

Versuch das. Wenn du es nicht hinkriegst, frag hier noch einmal und benenne das konkrete Problem.