Integral Nullstellen finden?
Die Aufgabe lautet:
Die Integralfunktion S f(t) dt hat vier Nullstellen. Geben Sie ungefähre Werte für diese Nullstellen an. (S= integralsymbol; untergrenze 2; obergranze x)
Die Lösung

Leider verstehe ich es mit der Lösung trotzdem nicht würde mich sehr freuen wenn mir jemand weiterhelfen kann. Vielen Dank schonmal
1 Antwort
Die Integralfunktion S f(t) dt hat vier Nullstellen.
Logisch. Wenn f(x) 3 Nullstellen hat, wie man ja sehen kann, muss die Funktion eine Potenz höher 4 Nullstellen haben. Die Ableitung hätte nur zwei Nullstellen.
S gibt die Fläche zwischen Gf und der x-Achse an.
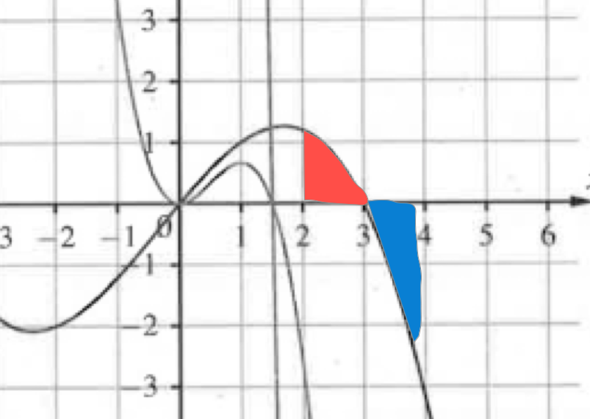
Wenn der Schüler etwas nicht versteht, macht er sich eine Skizze oder eine Tabelle. Hier wäre es eine Skizze, mit der wir zuerste die Nullstelle ganz rechts suchen. Dann muss die Fläche über der x-Achse (rot) gleich groß sein wie unter der x-Achse (blau):

Wir schätzen ab: rot ≈ 0,75 Kästchen
Damit blau ebenfalls ≈ 0,75 K hat, müssen wir etwa bei 3,8 den senkrechten Strich ziehen als Intergrationsgrenze.
Nun heben sich rot und blau gegenseitig auf und S = 0
x = 2 ist klar, denn dann gibt es gar keine Fläche und gar keine Fläche hat immer den Flächeninhalt 0.
Nach links macht man das genauso. Die Fläche von 0 bis 2 beträgt etwa 1,75 K. Von 0 ausgehend nach links ist die Fläche negativ und damit S = o wird, muss diese negative Fläche ebenfalls 1,75 K betragen. Das wäre in etwa bei -1,7 der Fall.
Noch weiter links gibts noch eine Stelle, an der sich positive und negative Flächen gegenseitig aufheben.
Wirklich vielen Dank