Die Funktion f' aufleiten?
Hallo. Ich habe eine Frage zur euch. Sieht die Funktion f wie eine Parabel aus? Ich mache gerade Hausaufgabe und ich benötige eure Hilfe. Vielen Dank im Voraus!

3 Antworten
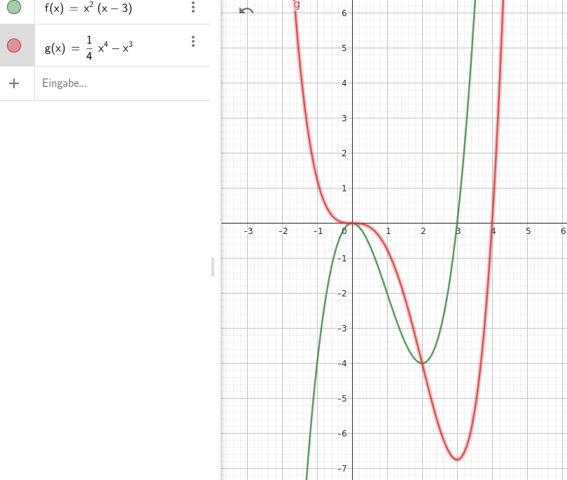
f ist eine Funktion 4. Grades, die von oben kommt und wieder nach oben verläuft
Bei ganzrationalen Funktionen ist die Aufleitung immer ein Grad höher
bei x=0 hat f einen Sattelpunkt (also Wendepunkt mit waagrechter Tangente) fallend/fallend
bei 2 hat f einen Wendepunkt
bei 3 hat f einen Tiefpunkt, da f' einen Vorzeichenwechsel von - nach + hat

f entspricht der Ableitung f'
g entspricht f
das rote Schaubild ist also die gesuchte Stammfunktion von f' (diese kann in y-Richtung beliebig verschoben werden)
f'(x) dieser Fkt wäre eine Parabel
Aber das Integral ist eine Fkt vierten Grades
Das ist eine Funktion dritten Grades. Also von der Form
f(x) = ax³ + bx² + cx + d
Die Stammfunktion ist dann eine Funktion vierten Grades.
Und die obige Funktion gibt die Steigung der Stammfunktion an.
Ja. Aber ich muss es graphisch aufleiten.