Aufleiten Aufgabe?
Hallo vielleicht kann mir jemand helfen bei der Aufgabe b..... Vielleicht kann mir allgemein jemand erklären wie das mit den Aufleiten funktioniert und wie ich Vorgehen soll..
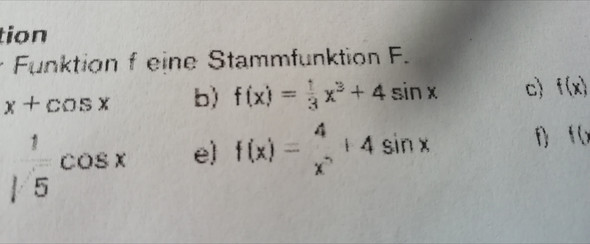
Bei der Aufgabe ist zur Funktion f die Stammfunktion gesucht. Danke für eure Hilfe!
4 Antworten
Erst einmal: Nein, es ist nicht jeweils die Stammfunktion gesucht, sondern eine Stammfunktion gesucht. Denn es gibt zu jeder Funktion unendlich viele Stammfunktionen, die sich voneinander jeweils additiv um eine Konstante unterscheiden.
Eine Stammfunktion F einer Funktion f ist eine Funktion, deren (erste) Ableitung gleich f ist. D.h. es soll F' = f sein.
Man sucht also bei Teilaufgabe b) eine Funktion F mit F'(x) = 1/3 x³ + 4 sin(x).
Überlege dir dazu, was abgeleitet 1/3 x³ ergibt, und was abgeleitet 4 sin(x) ergibt. Denke dabei daran, dass nach Potenzregel die Ableitung von xⁿ gleich n ⋅ xⁿ⁻¹ ist. Die Ableitung von sin(x) ist cos(x) und die Ableitung von cos(x) ist -sin(x).
Dementsprechend ...

Im konkreten Fall (Teilaufgabe b)) ist durch ...
F(x) = 1/12 ⋅ x⁴ - 4 ⋅ cos(x)
... eine entsprechende Stammfunktion gegeben.
Denn offensichtlich gilt dann F'(x) = f(x).
Bzw. ist auch durch ...
F(x) = 1/12 ⋅ x⁴ - 4 ⋅ cos(x) + C
... für eine beliebige Konstante C eine entsprechende Stammfunktion gegeben.
============
Du kannst dir dazu auch mal den folgenden Wikipedia-Eintrag ansehen:
https://de.wikipedia.org/wiki/Tabelle_von_Ableitungs-_und_Stammfunktionen

Die Lösung zu b ist 1/12 X^-4cos(x)
Überleg dir ei Fach was abgeleitet ergibt das u d wenn da zb ist x^3 steht dann ist die stammfunktion 1/4 x^4
Du solltest kennen :
f(x) = x^n => F(x) = (x^(n+1))/(n+1)) , n ≠ - 1
Es ist extrem wichtig, dass du die Bedingung
n ≠ 1 beachtest.
Beweis :
Nach dem HDI ist : f(x) = F'(x)
F(x) = (x^(n+1))/(n+1))
= 1/n+1 * x^(n+1)
F'(x) = (n+1)/(n+1) * x^n = x^n = f(x)
□
Beachte :
sin(x) => cos(x) "Ableitung"
sin(x) => -cos(x) "Integration"
* Edit : Beachte das die Menge aller Stammfunktionen gesucht wird, daher muss + C angehängt werden, wobei C ∈ IR ist.
Beim Ableiten fällt die Konstante weg.
Hilfestellungen gibt es reichlich im Internet:
https://www.mathebibel.de/stammfunktion
https://www.frustfrei-lernen.de/mathematik/aufleiten-beispiele-aufleitung.html
https://www.mathe-lerntipps.de/integral-aufleiten/
…, um nur einige zu nennen.