Wieso sind 1/3 eigentlich 33,333%?
Wieso sind 1/3 eigentlich 33,333% und nicht einfach 33% oder so?
Wie kann man das kurz erklärt mathematisch herleiten?
Edit : Wenn die Zahl hinter dem Komma immer weiter geht, is das doch niemals genau 100% , ist Mathematik dann nicht ganz minimal ungenau?
LG
7 Antworten
Dass 1/3 eine periodische Dezimalzahl ist, solltest Du wissen und daher ist das in Prozent:
"Herleiten" muss man da gar nichts.
Na wenn Du es sowieso weißt, warum fragst Du dann? Und was Dein Kommentar jetzt bedeuten soll, verstehe ich null. 3 * 33,33333..... ist 100%
Wenn die Nachkommastellen unendlich periodisch sind, dann fehlt doch immer eine unendliche 0,00001%. Das kommt mir ungenau vor
Nein. Das ist nicht ungenau. Das ist nur eine Folge der Dezimaldarstellung. Wenn du 1/3 in einem Zahlensystem darstellen würdest, dann könnte das eine abbrechende Dezimalzahl sein, so wie 1/5 im Zehnersystem.
Das Problem ist, dass in der Schule eigentlich nie wirklich richtig eingeführt wird, was eigentlich unendlich in diesem Kontext bedeutet. 0,Periode3 ist nicht eine Zahl, an die immer. noch was angefügt wird, sondern sie ist das Ergebnis dieses Prozesses. Die Folge
0,3
0,33
0,333
0,3333
usw. ist konvergent, sie konvergiert gegen eine fixe Zahl, ihren Grenzwert. Und dieser Grenzwert ist 0,Periode3. Daran ist nichts ungenau und es fehlt auch nix. Jedem einzelnen Wert der Folge fehlt was - aber dem Grenzwert der Folge nicht.
Du schaust sozusagen von draußen drauf: Das ist die Zahl, die rauskommt, wenn du das unendlich mal gemacht HAST. Dann bist du nämlich genau bei 1/3 angekommen. In der Schule wird das oft nur vage gesagt: man hängt immer noch was dran, man nähert sich an usw. Diese Sprechweise ist aber ungenau. Ich kann in der Mathematik ohne Probleme definieren, wo ich bin, wenn ich das unendlich oft gemacht habe (ohne das wirklich zu tun). Und wenn ich unendlich oft eine 3 angehängt habe, dann bin ich bei 1/3, nicht nur irgendwie nahe dran.
Wow. Tolle Antwort. Jetzt check ich die Theorie hinter dem ganzen auch endlich. Mathe ist schon spannend, wenn man nicht mehr zur "ungenauen" Schule geht. (: Toll!
Wenn ⅓ in einem anderen Zahlensystem dargestellt wird, ist es nicht unbedingt eine periodische Dezimalzahl. Z.B. im Dreiersystem ist es 0,1. Dafür sind dann ½, ⅕ und andere Zahlen periodisch.
😎
ist Mathematik dann nicht ganz minimal ungenau?
wenn "ungenau" auf Beherrschbarkeit abzielt, ist das die Untertreibung des Jahres - die Unendlichkeit der reellen Zahlen ist mächtiger als die der natürlichen Zahlen, oder anders ausgedrückt: es gibt zwischen 0 und 1 mehr reelle Zahlen als es überhaupt natürliche Zahlen gibt.
Man zeigt das, indem man eine unendliche, mit natürlichen Zahlen nummerierte Liste reeller Zahlen mit je unendlich vielen Stellen schreibt, in der jede reelle Zahl nur einmal vorkommen darf, und dann ein einfaches Verfahren vorführt, mit dem eine neue reelle Zahl in die Liste eingefügt wird, und das sicherstellt, dass diese neue Zahl keiner der vorhandenen gleich ist, maW die Liste kann nie vollständig sein.
es gibt zwischen 0 und 1 mehr reelle Zahlen als es überhaupt natürliche Zahlen gibt.
Wobei die Überabzählbarkeit der reellen Zahlen nichts mit der Periodizität von ⅓ zu tun hat.
Das Jahr ist noch lang. ='D
Achso, das macht für mich jetzt total Sinn. Das heißt, die reellen Zahlen sind wegen der Periodenlänge nicht ungenauer als 1/3 sondern sie sind sogar noch "unendlicher" als die rationalen Zahlen. Ich hoffe das darf man so sagen.
Die Mathematik ist konsistent und somit für die grundlegenden Axiome richtig.
Rechnest du 3,33... + 3,33... + 3,33... Mag es erscheinen 9,99... Zu ergeben, allerdings zieht sich das in die Unendlichkeit, sodass es sich dem Wert 1 annähert und in der Theorie auch annimmt. Das kann man sich halt nicht wirklich vorstellen...
Ja ich finde das sehr doof, weil mir quasi eine 0,0..1 % darin fehlt. Aber du meinst wegen der unendlichkeit ist das dann auf jedes "drittel" gleich verteilt?
Ja quasi. Stell es dir mehr so vor: 0,3 + 0,3 + 0,3 = 0,9. Da fehlt ja noch 0,1. Für die 0,1 rechnest du anteilig 0,03 + 0,03 + 0,03 = 0,09 noch drauf. Das ist aber wieder nicht 0,1 sonder halt 0,09 und so geht das weiter bis ins unendliche. Daher wird das in der Unendlichkeit angenommen. Das ist ziemlich kompliziert zu erklären weil Unendlichkeiten schwer zu verstehen sind.
funfact 0,333+0,333+0,333 = 0,999
aber 0,3periodisch + 0,3p + 0,3p = 1
und zwar genau 1^^ und nicht 0,9 periodisch
und 1/3 ist 0,3 periodisch
ist Mathematik dann nicht ganz minimal ungenau?
Gerade die Mathematik ist in diesen Fragen besonders streng. Deine Frage wird erschöpfend beantwortet mit den mathematischen Methoden der Grenzwertbildung. Wenn in der Schule das Stichwort "Limes" fällt und der Lehrer das Formelzeichen "lim" an die Tafel schreibt, dann solltest Du genau aufpassen.
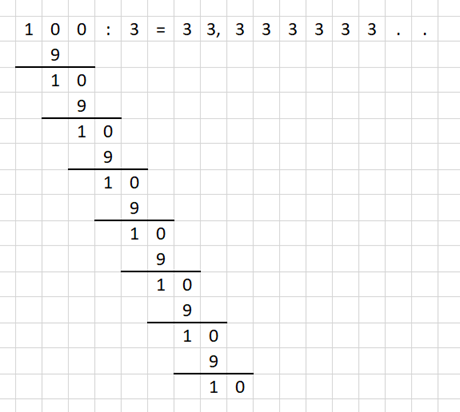
Vielleicht hilft Dir folgendes Beispiel der nie endenden schriftlichen Division.

Du kannst selbst bestimmen wie genau 1/3 als Dezimalzahl ausgedrückt werden soll. Sogar unendlich genau ist drin, wenn man die letzte "3" mit einem Überstrich verziert. Das ist die Vereinbarung für eine periodische (eine sich unendlich oft wiederholende) 3.
Hallo,
1/3 ist nicht 0,333 sondern 0,33 Periode. (Prozenz = Hundertstel)
Wenn du 0,33 als 1/3 haben würdest würde folgendes geschehen:
0,33 = 1/3 | *3
0,99 = 1 (das wäre falsch)
Wenn du das mit 0,333333 machen würdest wäre es genauer, allerdings immernoch nicht gleich 1. Dies geschieht erst mit 0,33 Periode, denn dabei handelt es sich um eine spezielle Schreibweise um bestimmte Zahlen überhaupt erst darstellen zu können. 0,99 Periode ist in dieser equivalent zu 1, womit die Rechnung aufgeht.
0,33 Periode = 1/3 | *3
0,99 Periode = 3/3 = 1
Mit besten Grüßen,
Codeline
Das weiß ich, aber dadurch nähert man sich ja nur der 100% an. Also ist das doch irgendwie voll ungenau.