Wie groß ist diese Fläche?
Hallo Leute!
Also folgendes:
Stellt euch mal einen Tetraeder vor, der so in einer Kugel liegt, dass eine Seite mit ihren 3 Eckpunkten genau auf der Kugeloberfläche sitzt. Die Kantenlänge des Tetraeders entspricht dem Kugelradius.
Nun wird ja auf die Kugeloberfläche ein gleichseitiges Dreieck projiziert.
Meine Frage ist nun:
Welche Fläche hat dieses Dreieck?
JTR
2 Antworten
Der Winkel zwischen den Kreissegmenten, die auf die Kugeloberfläche projiziert wird, ist etwa 1,231 rad. Mit der Formel für den Flächeninhalt eines Kugeldreiecks ergibt sich daraus eine Fläche von 0,5513 Flächeneinheiten bei einem Kugelradius von 1.

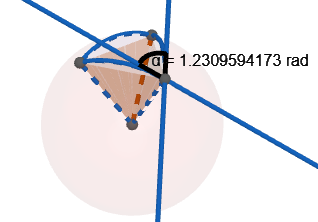
Nein, einfach glatt streichen geht nicht. Du musst, wie im Bild zwei Tangenten auf der Kugeloberfläche berechnen und dann den Winkel dazwischen bestimmen. Ich hab dafür jetzt der Einfachheit halber den 3D-Rechner von Geogebra benutzt. Der Winkel ist etwa 1,23 rad oder 70,52° (die Winkel an den Seiten eines Tetraeders haben nur 60°, daran siehst du, dass es nicht das Gleiche ist).
Dann gibt es die Formel für die Oberfläche eines Kugeldreiecks:
A = (α + β + γ - π) r²
Da die Seite des Tetraeders gleichschenklig ist und dementsprechend alle Winkel gleich groß sind, sind auch α, β und γ vom Kugelausschnitt gleich groß. Du kannst die Formel also vereinfachen zu A = (3α - π) r². Ich hab jetzt für die Kugel auch noch den Radius 1 gewählt. Dadurch ist r² = 1 und fällt in der Formel weg, wodurch sie nochmal vereinfacht wird zu A = 3α - π. Und da kommt eben die Fläche raus, die ich oben geschrieben hab.
Kommt auf den Durchmesser, Radius oder Fläche der Kugel!
Wenn man den Radius hat, hat man automatisch die anderen Größen.
Oberfläche einer Kugel ist ja 4Pi*R², Volumen ist 4PiR³/3 und der Durchmesser 2R
Okay, aber wie hast du dann die Fläche berechnet?
Integration?
Oder kann man tatsächlich das projizierte Dreieck nehmen, es "glatt streichen", sodass es wieder planar ist, und dann anhand der Kantenlänge die Fläche brechnen? Aber das verbietet einem ja eigentlich Gauß...