Problem beim Lösen einer Aufgabe mit einem Tetraeder?
Hallo
Ich bin eingentlich kein großer Fan davon, ganze Aufhaben bei gute Fragen zu posten. Wir müssen als Hausaufgabe folgede Audgabe lösen:
Gegeben sei ein reguläres Tetraeder T der Kantenlänge a. Man verlängert alle Kanten von T über alle Eckpunkte hinaus jeweils um a. Auf diese Weise entstehen zwölf neue Punkte. Wie groß ist das Volumen des von diesen zwölf Punkten wie in Abbildung A aufgespannten Körpers in Abhängigkeit vom Volumen V des Tetraeders T.
Im Anhang findet ihr die Abbildung A.
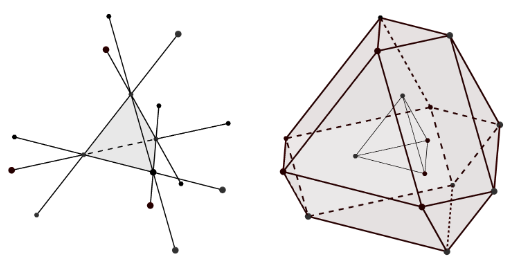
Ich habe einfach gar keine Ahnung, wie ich diese Aufgabe lösen soll. Habe schon versucht, Linien weiterzuziehen, geguckt, wie oft das Tetraeder in die neue Form passt, leider alles ohne Erfolg. Es entstehen immer andere Formen, wie z.B. ein Octaeder, mit dem ich auch nichts anfangen konnte.
Vielleicht könnt ihr mir da weiter helfen.
Danke im Voraus!
4 Antworten
Ich erkenne da 3 Objekte 5 gleiche Ursprungsflächen, 4 Vergrößerte und 4 die ich als Dach bezeichnen würde.
Eine Ursprungsfläche um die doppelte länge a vergrößert könnte auch das 10 fache sein.
Korrigiere auf 6 Dächer, würde dann 4 mal das Vergrößerte in die Formel einbauen plus 1 mal die Ursprungsfläche und 6 mal das Dach
Erste Variante:
Man könnte dies bspw. mit dem Satz von Gauß lösen:
https://de.wikipedia.org/wiki/Gau%C3%9Fscher_Integralsatz
Wähle hierzu bspw. als Vektorfeld:
F = (x, 0, 0)^T
damit folgt die Divergenz zu:
div(F) = 1
entsprechend folgt damit durch Anwenden des Satzes von Gauß:
Int[O]{ F*n dA } = Int[V]{ div(F) dV }
wobei O der Oberfläche des Körpers entspricht, n der Flächennormale, welche aus dem Volumen hinauszeigt, und V, dem Volumen des Körpers. Es folgt hier also durch einsetzen:
Int[O]{ F*n dA } = V
Wählt man nun das Koordinatensystem entsprechend geschickt, so lassen sich die Integrale relativ schnell berechnen ... .
Die zweite Variante basiert auf dem intuitiven Prinzip von Cavalieri:
https://de.wikipedia.org/wiki/Prinzip_von_Cavalieri
Hierzu zerschneiden wir den Körper in kleine Scheibchen der infinitesimalen Höhe dh und Querschnittsfläche A(h). Das so entstehende infinitesimale Volumen entspricht gerade: dV = A(h)*dh . Entsprechend lässt sich schreiben:
V = Int[-H, H]{ A(h) dh }
Man lege den Ursprung in die Mitte der unteren Fläche des ursprünglichen Tetraeders. Senkrecht dazu messe man die Höhe. Die Querschnittsfläche in der Höhe h berechnet sich dann einfach zu (lineare Abnahme der Kantenlängen mit der Höhe ... ):
H = sqrt(3)*a
A(h) = sqrt(3)*a²/4 + 3*sqrt(3)*(2a - a*h/H)²/4 = sqrt(3)*a²(1 + 3*(2 - h/H)²)/4
Einsetzen in das Integral liefert damit (beachte Symmetrie):
V = Int[-H, H]{ A(h) dh } = 2*Int[0, H]{ A(h) dh }
= 2*Int[0, H]{ sqrt(3)*a²(1 + 3*(2 - h/H)²)/4 dh }
= ... (da das Integral elementar ist erspar ich mir hier die Berechnung und Verweise nur auf Wolfram Alpha: https://www.wolframalpha.com/input/?i=Int%5B0%2C+H%5D%7B+sqrt%283%29*a%C2%B2%281+%2B+3*%282+-+h%2FH%29%C2%B2%29%2F4+dh+%7D
)
= 4*sqrt(3)*a²*H = 4*sqrt(3)*a²*sqrt(3)*a = 12*a³
Somit lautet das Volumen V:
V = 12*a³
Die dritte Variante basiert auf einer Zerlegung des Körpers in mehrere bekannte Teilkörper, was nun aber ohne Zeichnungen zu umständlich zu erklären wäre ... .
Hallo, ist das Ergebnis, das du bei der 2. Variante am Ende rausbekommst das endgültige Volumen des gesamten neu entstandenen Körpers?
Ja, sofern ich nicht irgendwo einen Flüchtigkeitsfehler gemacht habe.
Danke, das noch in Abhängigkeit des Tetraeders auszudrücken ist ja dann ein Kinderspiel dagegen
Vielleicht kommst du weiter, wenn du die drei zusätzlich entstehenden Körpertypen siehst:
- 4 gleiche Tetraeder wie das Original
- 6 langgezogene Pyramiden ("Dach"; weiss die korrekte Bezeichnung nicht)
- 4 Pyramidenstümpfe
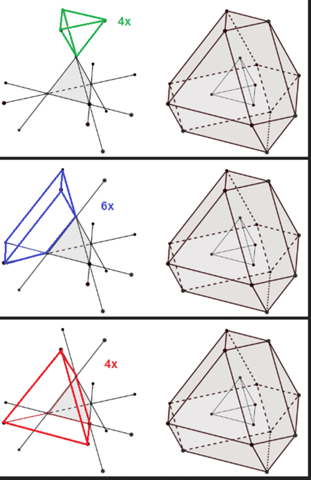
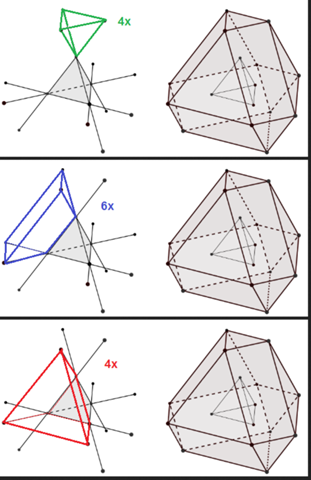
Alternativ Konstruktion


hm weil es sich um die 3 fache Verlängerung zur Ursprungsfläche Fläche handelt, wehr es doch denkbar das es sich dann um das 49 Fache der Ursprungsfläche handelt oder eine anderes wachstum .