Kann jemand diese Mathe Übung sehen?
In der folgenden Abbildung sind die Abmessungen eines ungespitzten Bleistifts angegeben. Ungespitzte Bleistifte haben den Graphit in einer zylindrischen Form, umgeben von Holz. Der Durchmesser des Graphits beträgt 2 mm. Die Dichte von Graphit beträgt 640 kg/m³. 40 cm Die Dichte des Holzes beträgt 420 kg/m³.
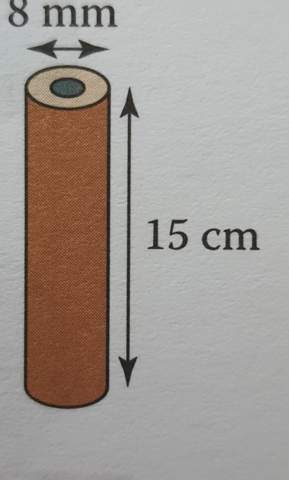
a) Finden Sie die Masse von 500 Bleistiften.
Meine Lösung:

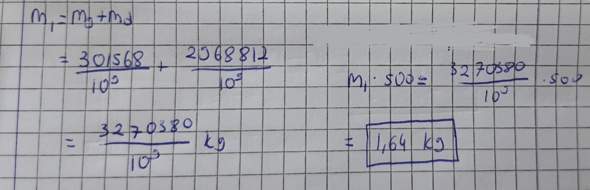
b)Geben Sie die Maße einer Schachtel an, die 500 Stifte aufnehmen kann.
Meine Lösung:

c)Wie viel Prozent des Volumens der Schachtel sind mit Stiften gefüllt?
(Icha kann diese Frage nicht lösen)
4 Antworten
Aufgabe a) Deine Rechnung ist richtig. Allerdings habe ich Anmerkungen mit den Einheiten. Die sind auch alle richtig, aber nicht greifbar. Du solltest die Masse von Graphit ausrechnen und bist auf das Ergebnis
M = 301568 kg * 10^-9 gekommen. Was sagt das aus? Was kann man sich darunter vorstellen?
Das ist das gleiche, als wenn ich dich fragen würde, wie viel du wiegst und statt 72 kg zu antworten, antwortest du: „Ich wiege 72.000 * 10^3 Milligramm. (???) Ja toll, aber das kann ich mir nicht vorstellen. Rechne den Graphit zusätzlich noch mal um in eine greifbare Einheit, hier Gramm. Der Graphitstab wiegt dann 0,3 g. Weiterer Vorteil ist, du kannst dein Ergebnis überprüfen. Der Holzstab ohne Graphit wiegt dann 3,0 g.
Aufgabe b)
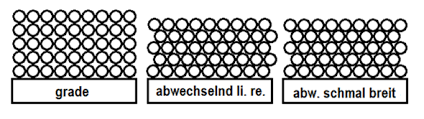
Hier sollst du die Maße der Packung finden, die 500 Stifte aufnehmen kann. Ein Stift ist dabei 15 cm lange. Deine Box hat jedoch eine Kantenlänge von 11 cm, was heißt, dass dort kein einziger Stift reinpassen kann. Sieh dir hierzu die Bilder an:
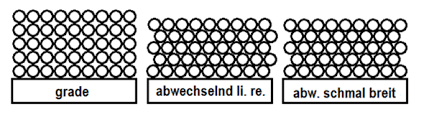
Das linke Bild beschreibt Kreise, wenn man die übereinander stapelt. Die beiden rechten Bilder sind annähernd gleich. Damit die Aufgabe nicht zu schwer wird, nehmen wir die linke Stapelweise, die jedoch aber auch am meisten Platz benötigt.
Die Tiefe der Kiste wird 15 cm lang sein, das entspricht der Stiftlänge. Zu bestimmen ist also noch die Höhe und die Länge der Kiste auf der Frontseite, so wie du es auf dem Bild siehst. Eine Maße der Kistenhöhe denke ich mir aus. Wenn ich 500 Stifte habe, könnte ich zum Beispiel 25 Stifte in der Breite stapeln und 20 Stifte in der Höhe. Dann hätte ich 20* 25 = 500 Stifte in der Box.
20 Stifte sind: 20* 8mm = 160mm breit.
25 Stifte sind: 25 * 8 mm = 200 mm lang.
Die Box hat also eine Größe von: Länge * Breite * Höhe = 200 mm * 160 mm * 150 mm
Aufgabe c)
Du kannst dir wieder das Bild anschauen. Die Zwischenräume sind noch frei.
Das Volumen der Box ist:
V = 200 * 160 * 150 mm³= 4.800.000 mm³ groß.
Die 500 Stifte haben ein Volumen von
V = 500 * pi * 4² * 150 m³ = 3.769.911 mm³
Füllungsgrad: 3.769.911 / 4.800.000 = 0,785 = 78,5%
(a) ich hätte md so gerechnet, damit du keine Rundungsfehler reinbekommst:(b) Länge 0,15m, Breite: 500·0,008m, Höhe: 0,008m (dabei lasse ich außer Acht, dass man die Zylinder vielleicht dichter packen könnte, wenn man mehrere Schichten macht, die zueinander versetzt sind...)
(c) Das Volumen der Schachtel wäre 0,15·500·0,008·0,008m³. Das Volumen der Stifte kennst du ja schon...
Hallo,
kommt drauf an, wie die Stifte gestapelt werden.
Wenn Du sie auf Lücke stapelst, nehmen zwei Lagen weniger als 1,6 cm (2*8 mm) in der Höhe ein, sondern etwa 1,5 cm (bißchen weniger).
Zwei Lagen übereinander ergeben aber immer einen Stift weniger als zweimal eine Lage.
Wenn Du etwa unten 25 Stifte nebeneinander legst, passen eine Lage darüber nur 24 Stifte in die Lücken. Darüber kommt wieder eine Lage mit 25 Stiften, dann 24, immer abwechselnd.
Günstig wären vielleicht abwechselnde Lagen von 27 und 26 Stiften, also 53.
500:53=9,434, also etwa 9,5 Doppellagen oder 19 einzelne. So käme die Schachtel auf eine Höhe von etwa 13,3 cm, nämlich 18*4*Wurzel (3)+2*4 mm.
Wenn die Stifte auf Lücke gestapelt werden, bilden die Mittelpunkte von jeweils drei benachbarter Stifte - zwei nebeneinander unten und einer auf Lücke darüber - ein gleichseitiges Dreieck mit der Höhe (a/2)*Wurzel (3) und a=0,8 cm.
Die unteren Mittelpunkte sind 0,4 cm vom Boden der Schachtel weg, die oberen der obersten Lage 0,4 cm vom Deckel.
27 Stifte nebeneinander ergeben 27*0,8 cm =21,6 cm die Breite der Schachtel.
Die Tiefe ist natürlich 15 cm, die Länge eines Stiftes.
Mögliche Maße der Schachtel in Breite mal Tiefe mal Höhe wären somit
21,6*15*13,3 cm³.
Dieses Volumen kannst Du ins Verhältnis setzen zum Nettovolumen der 500 Zylinder mit Radius 0,4 cm und Höhe 15 cm.
Kann sein, daß die Schachtel noch günstigere Ausmaße haben könnte vielleicht mit einer Lage mehr und dafür weniger Breite.
Herzliche Grüße,
Willy
a) stimmt.
so würde ich das rechnen:
b) Es wird nur nach einer Schachtel und nicht nach einer bestimmten Schachtel gefragt. In meiner Schachtel liegen die Bleistifte übereinender:
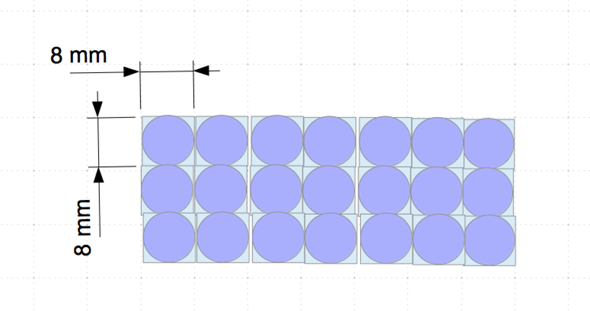
Dabei liegen 50 Bleistifte nebeneinander und 10 übereinander.
Breite der Schachte: 8 mm * 50 = 400 mm = 40 cm = 0,4 m
Höhe der Schachtel: 8 mm * 10 = 80 mm = 8 cm = 0,08 m
Länge der Schachtel: 15 cm
Volumen der Schachtel V:
V = 40 cm * 8 cm * 15 cm = 4800 cm^3 = 4,8 l
c)
Das Volumen eines Bleistiftes beträgt:
V = π r^2 * h = π * (0,4 cm)^2 * 15 cm = 7,540 cm^3
Volumen von 500 Bleistiften:
Vges = 500 * 7,540cm^3 = 3770 cm^3
3770 cm^3 von 4800 cm^3 sind 3770/4800 = 0,785 = 78,5 %
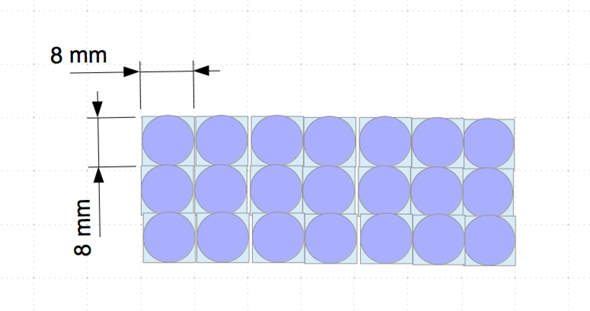
Aber c kann ich nicht rechnen. Also die Volum der Schachtel ist = 0.0048 und die Volum der Bleistiefel ist 0.0000075 oder?