Satz des Pythagoras?
Hallo Leute,
Und zwar hab ich die Aufgaben Nr. 16&17 bearbeitet und wollte euch fragen ob sie richtig gelöst sind. Ich hab das so gerechnet, wie ich glaube das es richtig ist. Obwohl ich mir sehr unsicher dabei bin, weil ich das selber nicht wirklich verstanden hab. Ich würde mich sehr über eure Hilfe freuen :)


4 Antworten
Bei Aufgabe 16 hat sich meiner Meinung nach ein Fehler eingeschlichen. Bei dieser Art Leiter bildet sich ein gleichschenkliges Dreieck. In diesem "trifft" die Höhe die Mitte (!) der Grundseite. Du musst also nicht mit 1,4m rechnen, sondern mit 70cm.
Schau Dir doch mal das Bild an neben der Aufgabe. So sieht die Leiter aus. Da ist nirgends ein rechter Winkel - Du darfst den Satz des Pythagoras hier gar nicht anwenden. Das rechtwinklige Dreieck (genauer: die beiden rechtwinkligen Dreiecke) entstehen erst durch das Einzeichnen der Höhe, was eine Senkrechte ist, die durch die Spitze der Leiter geht. Und die teilt nunmal die Strecke zwischen beiden Schenkeln genau in der Mitte - also bei 70cm.
Zu Deiner zweiten Frage: Ist denn (70cm)² + (170cm)² = (310cm)²?
Ich glaube nicht das meine Lösung richtig ist meinte ich.
Nein, die Proberechnung, mit der Du ganz einfach herausfinden kannst, ob 1,7m korrekt ist. Das war ja Deine Frage.
Ok danke ich meinte dann das das nicht richtig ist
Naja, Du rechnest sie halt einfach nochmal, nur mit 70cm anstatt mit 140cm. Wenn Du sie zuvor alleine gemacht hast, dann schaffst Du das doch jetzt auch alleine...
Ja, alles gut, ich hab nur nicht verstanden was jetzt genau das richtige ist weshalb ich gefragt habe wie es verbessert ist.
Ja stimmt.
Bei (17) nennt man das auch das Prinzip des Maurerdreieck 3 | 4 | 5.
3 geteilt durch 4 ist 0,75. 90 geteilt durch 120 ist 0,75. Also Maurerdreieck.
Wir hatten noch nie glaub ich das Prinzip des Maurerdreieck.
Das ist ein direktes Ergebnis aus dem Satz des Pythagoras. Man wählt die Größen so, dass im Satz des Pythagoras glatte Zahlen rauskommen.
Noch einmal zum Pythagoras
in dem gleichschenkligen Dreieck soll die Höhe berechnet werden. Die höhe steht bekanntlich senkrecht auf den 140cm. Zugleich ist die Höhe auch winkelhabierende. Dadurch teilt die Höhe gleichzeitig auch die 140er Seite in 2 mal 70cm und 2 rechtwinklige Dreiecke. Der Pythagoras wird ja bei solchen Dreiecken angewendet.
Bekannt ist eine Kathete 70 und Hypothenuse 310 fehlt h
h*h + 70*70 = 310 * 310
Der Satz die Summe der Kathetenquadrate ist gleich dem Hypothenusenquadrat oder auch die Summe der Flächeninhalte der Kathenquadrate ist gleich der Fläche des Hypothenusenquadrats.
Siehe auch 3*3 +4*4 = 5*5
Zu Deinem Kommentar "Ich verstehe aber noch nicht wieso ich mit 70cm rechne?"
Weil das rechtwinklige Dreieck (und nur für solche gilt der Satz des Pythagoras) das rot eingezeichnete Dreieck ist. Der rechte Winkel ist dort, wo ein vertikale Linie von der Spitze der Leiter den Boden in der Mitte (1,4 m / 2 = 0,7 m) der beiden Leiterarme trifft-
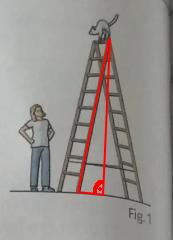
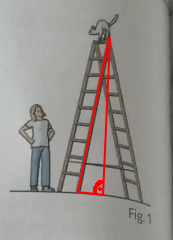
Ich verstehe aber noch nicht wieso ich mit 70cm rechne? Kommt da 1,7m raus?