Mathe?
Kann mir bitte wer Aufgabe 1 erklären. Ich habe schon viele Videos etc. geguckt aber checke es nicht.

Bitte nicht zu kompliziert schreiben. Sondern am liebsten so simpel wie möglich halten.
Ich möchte hier niemanden zu viel Arbeit aufdrängen aber könnte einer vielleicht das ganze auf Papier aufschreiben weil es somit für mich besser nachvollziehbar ist. Danke
3 Antworten
Andere haben Dir schon gezeigt, wie man die Aufgabe in ein lineares Gleichungssystem umwandeln kann, das man dann mit Gauß oder sonstwie löst.
Es gibt aber auch eine fix&fertige Formel dafür, die auf Lagrange zurückgeht und in die man nur einsetzen muß. Für ein quadratisches Polynom, das durch die Punkte (x₁|y₁), (x₂|y₂) und (x₃|y₃) gehen soll, lautet sie

und man verwendet sie gerne zum Interpolieren oder numerischen Differenzieren von Tabellendaten.
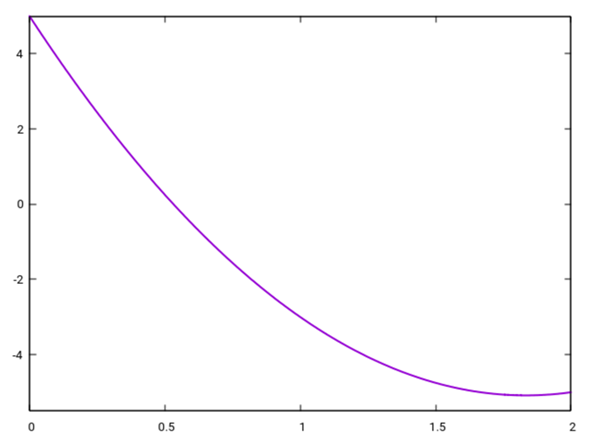
So kann ich das Polynom ganz leicht mit Gnuplot zeichnen:

x1=1;y1=-3; x2=0;y2=5; x3=2;y3=-5
plot [0:2] [-5.5:5] (x-x2)*(x-x3)/(x1-x2)/(x1-x3) * y1 + (x-x1)*(x-x3)/(x2-x1)/(x2-x3)*y2 + (x-x1)*(x-x2)/(x3-x1)/(x3-x2) * y3 lw 2 title ""
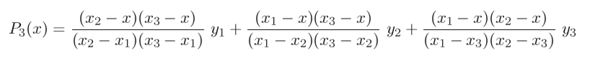
Ich gebe Dir recht, für die Schule ist das wahrscheinlich nichts. Andererseits fiel mir das sofort als unorthodoxer Lösungweg ein, weil ich selber mal mit dieser Methode gearbeitet habe.
Du stellst ein Gleichungssystem mit drei Gleichungen auf.
3 = a*1² + b*1 + c (Erster Punkt)
5 = a*0² + b*0 + c (Zweiter Punkt)
-5 = a*2² + b*2 + c (Dritter Punkt)
Dann löst du das Gleichungssystem mithilfe der drei dir hoffentlich bekannten Verfahren (Einsetzungs-, Additions- und Gleichsetzungsverfahren) um a, b und c herauszubekommen.
Wenn du Werte für a, b und c hast schreibst du diese Werte in die Grundstruktur der Normalform f(x) = ax² + bx + c
Um die Probe durchzuführen setzt du dann in x die x Koordinate eines deiner Punkte ein und schaust ob für f(x) deine y Koordinate rauskommt. Wenn ja dann stimmt die Probe und du hast die Werte für a, b und c richtig berechnet
Du nimmst für die Unbekannten die Variablen a, b, c
Deine Gleichung hat grundsätzlich die Form
ax²+bx+c=irgendwas
So, jetzt hast du Punkte, Punkte sind x und y werte.
Nehmen wir zb den Punkt 1/3
Also ist für den x Wert 1, der y wert=3
Dann machen wir daraus
a mal 1²+b mal 1+c=3, weil der y Wert 3 ist
also a+b+c=3
das machen wir mit allen punkten und haben dann 3 gleichungen mit 3 Unbekannten
das lösen wir mit einem Verfahren auf.
Einsetzungsverfahren wahrscheinlich.
Eigentlich ist es ziemlich einfach, viele haben nur eine Blockade mti den zusätzliche Variablen.
Aber wenn man das Begriffen hat, ist das nicht irgendwie schwierig.
Die Gefahr bei solchen Formeln ist, dass man den Sachverhalt gar nicht verstanden hat und Mathematik für etwas hält, das so kompliziert ist, weil man soetwas schwer auswendig lernen kann.