Kann jemand erklären wie man hier den Grenzwert berechnet? Ich habe einfach keine Ahnung wie ich hier vorgehen soll?
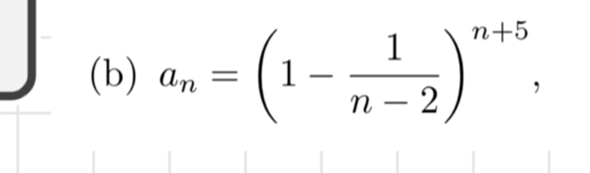
2 Antworten
a_n = (1 – 1 / (n – 2))^(n+5)
a_n = ((n – 3) / (n – 2))^(n+5)
[Prüfen, ob überhaupt konvergiert.]
[1. Beschränktheit]
0 ≤ (n – 3) / (n – 2) ≤ 1
0^(n+5) ≤ ((n – 3) / (n – 2))^(n+5) ≤ 1^(n+5)
0 ≤ a_n ≤ 1
[2. Monotonie (wachsend)]
a_(n+1) > a_n
((n – 2) / (n – 1))^(n+6) > ((n – 3) / (n – 2))^(n+5)
(n – 2) / (n – 1) ((n – 2) / (n – 1))^(n+5) > ((n – 3) / (n – 2))^(n+5)
(n – 2) / (n – 1) > ((n – 1) (n – 3) / (n – 2)²)^(n+5)
1 – 1 / (n – 1) > (1 – 1 / (n – 2)²)^(n+5)
[Anwenden Bernoulli-Ungleichung]
1 – 1 / (n – 1) > 1 – (n + 5) / (n – 2)²
(n + 5) / (n – 2)² > 1 / (n – 1)
(n + 5) (n – 1) > (n – 2)²
n² + 4 n – 5 > n² – 4 n + 4
n > 9 / 8 (n ≥ 3)
[Monotoniekriterium (für Folgen) ist erfüllt, es gibt also (genau) einen Grenzwert.]
[Grenzwert berechnen.]
a_n = (1 – 1 / (n – 2))^(n+5)
a_(n+2) = (1 – 1 / n)^(n+7)
a_(n+2) = (1 – 1 / n)^7 • (1 – 1 / n)^n
a_(n+2) = b_n • c_n
[mit den Definitionen:]
b_n := (1 – 1 / n)^7
c_n := (1 – 1 / n)^n
[Wenn b_n und c_n beide konvergieren, konvergiert auch a_n (Rechengesetz für Folgen). Wir zeigen also, dass b_n und c_n konvergieren, um den Grenzwert für a_n anzugeben.]
[Grenzwert b_n berechnen]
b_n = (1 – 1 / n)^7
1 – 1 / n —> 1 (n —> ∞)
[Anwenden Rechengesetz (siehe Link oben)]
b_n = (1 – 1 / n)^7 —> 1^7 = 1 (n —> ∞)
[Grenzwert c_n berechnen]
c_n = (1 – 1 / n)^n
[Bekannte Folge, (1 + x / n)^n ist die Folge, die gegen e^x geht, also folgt:]
c_n —> e^(–1) = 1 / e (n —> ∞)
[Es konvergieren also beide Folgen, also ist der Grenzwert von a_n einfach...]
a_n = b_n • c_n —> 1 • 1 / e = 1 / e (n —> ∞)
Ich würde es umstellen:
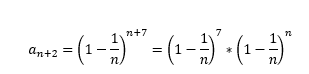
Der Grenzwert ist 1/e.
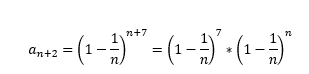
Ja, die Aufgabe ist nicht ganz einfach. Da muss manch ein Gedankengang erstmal sacken.
Es ist eine Indexverschiebung: Ich gehe einfach 2 Folgenglieder weiter. Das spielt für das Verhalten im Unendlichen keine Rolle: Auf der linlen Seite habe ich n+2. Da muss ich rechts auch überall n um 2 erhöhen. Das habe ich so gewählt, damit die -2 im Nenner verschwindet.
Ich kriege es einfach nicht gebacken :(.
wäre es möglich, dass du mir das vorrechnest oder es mir irgendwie erklären könntest. Ich würde es richtig gerne verstehen
Hallo, ich weiß die Rückmeldung kommt etwas spät aber kannst du mir mal erklären wie du auf n+7 im Exponenten kommst?