f(x)=x^2-6x-8?
Ich muss die Gleichung in ein Koprdimatensstem eintragen, aber wie mache ich das? muss ich die erst irgendwie ausrechen, denn zusammenfassen kann ich das x^2 mit 6x doch gar nicht?
2 Antworten
wenn du die Scheitelpunktsform oder die pq-Formel nicht kennst , musst du eine Wertetabelle anfertigen - Hättest du die ( teile es uns mit ) , wüsstest du , wo die "Mitte" , der Scheitelpunkt liegen muss.
Beginne bei x = 0
denn zusammenfassen kann ich das x^2 mit 6x doch gar nicht?
natürlich nicht
0² - 6*0 - 8 = 0 - 0 - 8 = -8
nun x = 1
1² - 6*1 - 8 = -13
probiere nun x = -1
(-1)² - 6*-1 - 8 = 1 + 6 - 8 = -1
Zeichne die Punkte ein

jetzt solltest du erkennen können , dass die Par etwa so verläuft . Es ist also sinnvoll mit x = 2 , 3 , 4 weiterzumachen
Den exakten Scheitelpunkt trifft man hier zwar , aber das ist nicht immer so .
.
TRICK ! schau dir die Zahl vor dem x an . Hier -6 . Halbiere sie und ändere das Vorzeichen ::::: + 3
nun hast du den x-Wert des Scheitels und kannst eine Wertetabelle von x = -1 bis x = 7 anfertigen
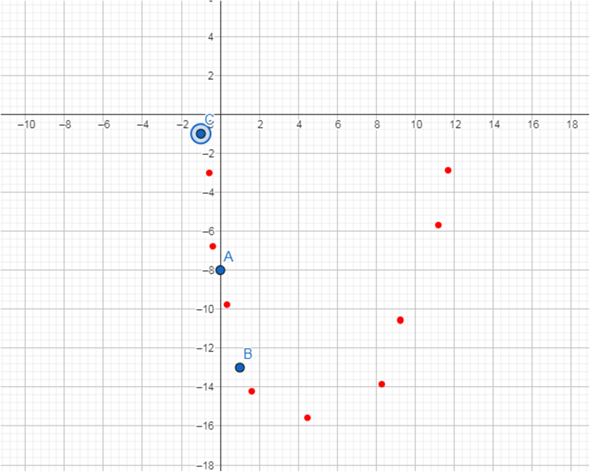
Wenn man den Trick nicht kennt , ist es mit einer reinen Wertetabelle sehr mühsam
Es wäre noch zu bemerken, dass der Trick nur funktioniert, wenn vor dem x² kein Faktor steht. Ansonsten müsste man die Zahl vor dem x nicht nur halbieren, sondern zusätzlich noch durch diesen Faktor teilen.
Was dann aber natürlich immer noch besser ist, als mit einer reinen Wertetabelle herumzustochern! 😉
Wenn du die Parabel in die Scheitelpunktform bringst, kannst du die Koordinate des Scheitelpunktes ablesen; das Vorzeichen vor dem quadratischen Glied gibt dir darüberhinaus die Information, ob die Parabel nach oben oder unten geöffnet ist.
Wenn du jetzt noch die Nullstellen ermittelst oder einfach ein paar Koordinaten mehr berechnest (idealerweise, indem du "einfache" Zahlen einsetzt), kannst du die Parabel recht gut skizzieren.
Nachtrag: Angesichts deiner Bemerkung über das Zusammenfassen von x² und 6x vermute ich, dass dir die Grundlagen über Parabeln fehlen. Wenn du keine Ahnung hast, von was ich oben überhaupt geredet hast, könntest du natürlich einfach einen Schwung Koordinaten ausrechnen, eintragen und diese kreativ miteinander verbinden, was je nach Wahl der Punkte ein mehr oder weniger gutes Ergebnis liefert, aber die bessere Taktik wäre, dich näher mit Parabeln zu befassen. Vermutlich kommst du da ohnehin nicht drumrum, daher, je früher du dich damit beschäftigst desto besser.
2. Nachtrag (s. Kommentar):
Trügerische Funktion #1:


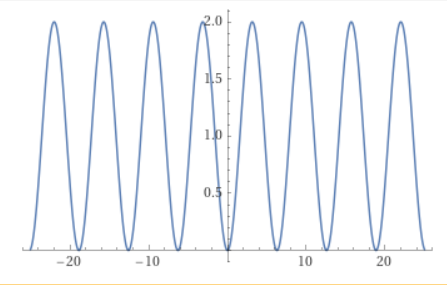
Trügerische Funktion #2:




Ich danke dir für deine ausführliche Nachricht, nur leider kann ich sie überhaupt nicht verstehen. muss ich bei so einer aufgaben eine wertetabelle machen? also das mit 1 2 3 0 -1 -2 -3 und dann die ergebnisse eintragen und verbinden? oder muss ich die nullstelle ausrechnen? also das mit 0=x^2-6x-8|+8 ….
Ja, das dachte ich mir schon, dass du mir nicht folgen kannst (s. mein 1. Nachtrag).
Wenn du im Unterricht nicht komplett gepennt hast, vermute ich, dass das was ihr im Moment macht, Vorbereitungen auf die Einführung von quadratischen Funktionen ist. Wenn dem so ist, wirst du das, was ich geschrieben habe, dann in ein paar Wochen oder Monaten verstehen! 😉
Wenn ich mich also nicht täusche, dann ist es genau das, was du vermutet hast, dann sollst du einfach nur eine Wertetabelle erstellen, die Punkte in das Koordinatensystem eintragen und verbinden.
Allerdings wirst du sehen, dass das keine gerade Linie ergibt, sondern eine Kurve. Die musst du dann eben so einzeichnen, dass sie durch die Punkte, die du mithilfe der Wertetabelle errechnet hast, gehen.
Im Prinzip ist es so, dass du die Funktion umso genauer zeichnen kannst, je mehr Koordinaten du berechnest und je enger diese zusammen liegen, ist ja auch logisch.
Andererseits hat man aber auch keine Lust Hunderte oder Tausende von Koordinaten zu berechnen, deshalb wird so eine Zeichnung vermutlich nie 100%ig richtig sein, das erwartet dein Lehrer aber auch nicht.
Allerdings kann man beim Skizzieren auch in Fallen tappen. Diese kann man vermeiden, wenn man sich mit den entsprechenden Funktionen besser auskennt. Den Text, den ich oben geschrieben habe und den du (noch) nicht verstanden hast, sollte dir helfen, solche Fallen zu vermeiden.
Im vorliegenden Fall ist es so, dass du eine Parabel herausbekommst (so nennt man die Form solch einer quadratischen Funktion), die annähernd wie ein U aussieht. Wenn du nun aber z.B. nur Koordinaten berechnest, die auf einer Seite dieses U's liegen (man spricht dann von einem Ast der Parabel), dann wüsstest du vermutlich gar nicht, dass die komplette Form wie ein U aussieht.
Ich habe dir oben in einem 2. Nachtrag mal als Beispiel noch zwei "trügerische" Funktionen eingefügt, die in beiden auch aussehen wie eine Parabel - bis man dann herauszoomt und sieht, dass es ganz anders weitergeht!
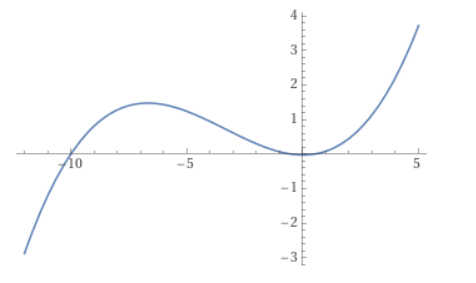
Im ersten Fall handelt es sich um eine Funktion 3. Grades mit folgender Funktionsgleichung:
f(x) = 1/100 x³ + 1/10 x² - 1/400 x - 1/40
Wie du siehst, ergibt sich zwischen -2 und 1,7 ein Graph, der auf den ersten Blick aussieht, wie eine wunderschöne Parabel, aber wenn man die Wertetabelle ausweitet, erkennt man, dass die Funktion weiter links einen weiteren Haken schlägt und nach unten abbiegt.
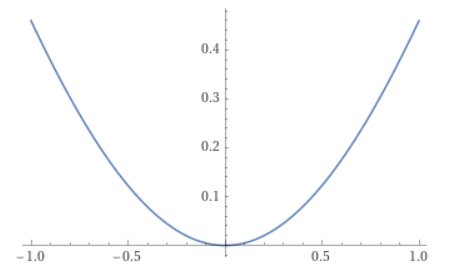
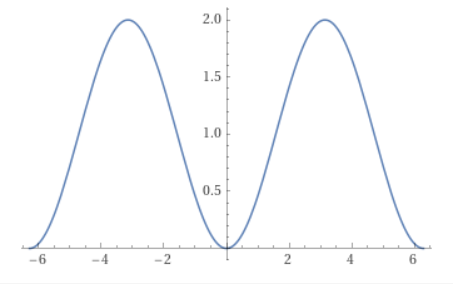
Im zweiten Fall handelt es sich um die Funktion -sin(x+π/2)+1, die zwischen -1 und +1 ebenfalls aussieht wie eine perfekte Parabel. (sin steht hier für die Sinusfunktion.)
Aber wenn man den Bereich der Funktion links und rechts ein bisschen erweitert, sieht man, dass man hier zufällig ein Tal zwischen zwei "Bergen" erwischt hat, und wenn man den Bereich noch weiter nimmt, dann erkennt man, dass es sich um eine Funktion handelt, die immer zwischen den Werten 0 und 2 oszilliert. Das hat dann mit einer Parabel überhaupt nichts mehr zu tun.
Solange man sich mit den jeweiligen Funktionen nicht auskennt, muss man eben hoffen, dass man einen einigermaßen sinnvollen Bereich der Funktion skizziert.
Hinweis für den Fragesteller: Die x-Koordinate des Scheitelpunkts liegt genau in der Mitte zwischen den Nullstellen. Die y-Koordinate kann man dann ausrechnen.
Achso, ich glaube ich hab es verstanden, ich war einfach wegen der hohen zahl verunsichert und hab es auf die flasche achse geschrieben, deswegen sah das so falsch aus. Vielen dankk