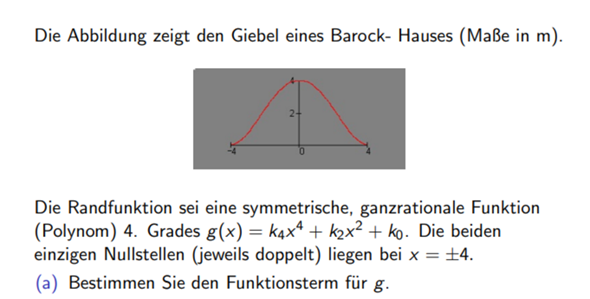
Funktionsterm aus Randfunktion berechnen?

Wie gehe ich vor ? In x die Nullstellen 4 und - 4einsetzen? Und wenn ja, wie weiter?

Answer 1

[Halbrecht]

Erster Ansatz nach Schema F , g(x) und g'(x) nutzen

.

k0 = 4 

.

g(4) = 0 

0 = 256a + 16b + 4

.

g'(4) = 0 

0 = 256a + 8b 

.

g(x) = 1/64 * x^4 - 1/2 * x² + 4 

.

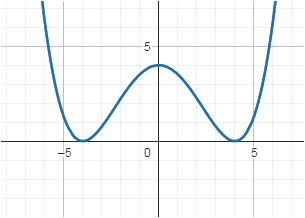
Probe 

.

.

Andere Möglichkeit

g(x) = a * (x+4)² * (x-4)²

Nun ( 0/4 )  einsetzen 

Comments

[oioioi5]

Wieso quadrierst du die Terme in Klammern bei der anderen Möglichkeit?

[Halbrecht]

@oioioi5

d o p p e l t e Nullstellen . Das sind dann Berührstellen . Graph hat zwar den y - Wert Null dort , schneidet die x-Achse aber nicht

Dass der Graph rechts und links wieder hoch geht muss man eben aus "doppelt" erschließen . Der eigentliche Clou der Aufgabe.

.

[oioioi5]

@Halbrecht

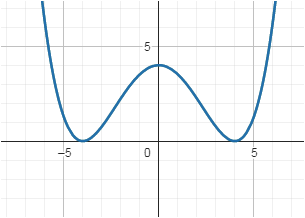
Ok danke, ich bin jetzt grade noch etwas verwirrt weil einmal die Nullstellen (-4I0) bzw (4I0) gegben sind und der Scheitelpunkt (0I4) , also beides Punkte mit 0 und 4.

Setzt du da bei k0 jetzt die 4 vom Scheitelpunkt oder Nullstelle ein?

[Halbrecht]

@oioioi5

guck hin . Der Graph geht bei x = 0 bei y = 4 durch die yAchse . Also den SP

Ja , ich hasse auch die Aufgaben ,wo immer wieder dieselben Zahlen vorkommen.Wenn ich Beispiele konstruiere, versuche ich das zu vermeiden, damit vieles eindeutig identifizierbar ist .

[oioioi5]

@Halbrecht

Danke, ich bleibe mal bei der Methode mit der Nullstellenform, wie gehe ich vor nach dem ich a (1/64) bestimmt habe? Tut mir leid aber ich habe wirklich keine Ahnung und wäre froh diese Aufgabe einfach irgendwie durchzukriegen.

[Halbrecht]

@oioioi5

habe ich jetzt geschrieben .

Viel spaß beim ausmultiplizieren , echt viel zu tun :))

.

Und dran denken : Diese Aufgabe ist ein Spezialfall. Schema F sollte man drauf haben . Ist viel häufiger nötig

[oioioi5]

@Halbrecht

Ich versteh leider wirklich nicht wie du von 0 = 256a + 16b + 4 auf 0 = 256a + 8b  kommst und im nächsten Schritt dann auf den Term g(x) = 1/64 * x^4 - 1/2 * x² + 4 

Answer 2

[Maxi170703]

Schreib die Funktion als Produkt von Linearfaktoren und multipliziere dieses mit einer passenden Konstante.

Woher ich das weiß: Studium / Ausbildung – Maschinenbaustudent, RWTH Aachen

Comments

[oioioi5]

Hey wo du das grade sagst ist mir eines aufgefallen: Ist die Linearfaktorzerlegung nicht das selbe wie "in Nullstellenform bringen"?

[Maxi170703]

@oioioi5

Nullstellenform könnte ein umgangssprachlicher Ausdruck für die Linearfaktorzerlegung sein, da die einzelnen Linearfaktoren für gewöhnlich mithilfe der Nullstellen gebildet werden.

Answer 3

[Niemand18]

Nutz die Nullstellenform und dem Punkt P(0/4) um dann „a“ auszurechnen. Achte auf die Vielfachheit!

Woher ich das weiß: Hobby – Selbststudium

Comments

[oioioi5]

Ich bekomm a (k4) = 1/4 raus, ist das richtig? Und wie gehe ich mit b und c vor?

[Niemand18]

@oioioi5

Nullstellenform ! f(x) = a*(x-x1)^v * (x-x2)^v‘, wobei v,v‘ die Vielfachheiten sind und x1,x2 deine Nullstellen. Alles einsetzen und dann das a richtig berechnen.

[oioioi5]

@Niemand18

Was bedeutet ^v?

Also ich stelle das so auf (Punkt (0I4) eingesetzt):

4 = a * (0-4) * (0+4)

Ist das nicht richtig?

[Halbrecht]

@oioioi5

nein ,die exponenten vergessen.

[Halbrecht]

@oioioi5

nein , 1/64

[oioioi5]

@Halbrecht

Wie gehts dann weiter? a= 1/64 wie mache ich jetzt weiter?

[Halbrecht]

@oioioi5

Andere Möglichkeit

g(x) = a * (x+4)² * (x-4)²

Nun ( 0/4 ) einsetzen 

dann ausmultiplizieren

1/64 * (x² + 8x + 16)(x²-8x+16)

oder

1/64 * (x+4)(x-4)(x+4)(x-4) = 1/64 * (x²-16)(x²-16)

.

Da geht ja meine erste Methode , schmema F , viel schneller.

[oioioi5]

@Halbrecht

Bitte nenn mir noch den Namen vom Schema F, wie diese Rechenmethode heißt

[Halbrecht]

@oioioi5

Das ist ein lineares Gleichungssystem (kennst du noch von : zwei Glg mit 2 Unbekannten ) . Hergestellt auf den Bedingungen so wie sie in meiner Antwort stehen. Aber kann sein ,dass ihr das noch bekommt .Da bin ich mDann ist diese Frage hier eine , die euer Wissen um doppelte Nullstellen abprüfen sollte.

.

das ist da Thema

Answer 4

[MeisterRuelps, UserMod Light]

Du hast einen Extrempunkt, den Du nutzen kannst.