Fundamentalsystem einer DGL?
Hallo,
wie bestimme ich ein reelles Fundamentalsystem für das DGL-System
?
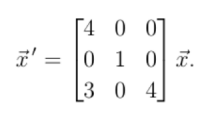
Für die Beantwortung meiner Frage bedanke ich mich im Voraus.
2 Antworten
Probier es mit dem Ansatz
x(t) = w e^(a x),
wobei w Eigenvektoren zu zugehörigen Eigenwerten a der Matrix sind. Das Fundamentalsystem ist dann (bei verschiedenen einfachen Eigenwerten)
{w1 e^(a1 t), w2 e^(a2 t), w3 e^(a3 t)}
Denn es gilt beim Ansatz x(t) = w u(t),
w u'(t) = x'(t) = A x(t) = A w u(t) = a w u(t),
also u'(t) = a u(t), was zu u(t) = e^(a x) führt.
Wir brauchen also die Eigenwerte und -vektoren. Wie man die berechnet, weißt du sicherlich. Du erhält dann das charakteristische Polynom
det(A – z E) = 0
(z – 1) (z – 4)² = 0.
Eigenvektor zum Eigenwert 1 ist
Ker(A – 1 E) = span((0, 1, 0)),
zum Eigenwert 4 ist es
Ker(A – 4 E) = span((0, 0, 1)).
Bis jetzt sieht unser Fundamentalsystem so aus: {(0, 1, 0) e^t, (0, 0, 1) e^(4 t)}.
Jetzt ist 4 aber doppelter Eigenwert (Vielfachheit im charakteristischen Polynom ist 2), aber die Lösung
(1, 0, 0) e^(4 t)
zweimal aufzuschreiben bringt uns natürlich nicht weiter.
Daher müssen wir den Ansatz
x(t) = ((1, 0, 0) + (0, 0, 3) u(t)) e^(4 t)
machen mit
b = (A – 4 E) (0, 0, 1) = (0, 0, 3)
So kommt man dann auf
u(t) = t.
Das Fundamentalsystem lautet somit
{(0, e^t, 0), (e^(4 t), 0, 0), (e^(4 t), 0, 3 t e^(4 t))}.
Das ist ein gewöhnliches System mit konstanten Koeffizienten. Du bestimmst die Eigenwerte und zu jedem Eigenwert gehört eine Lösung der DGL. In diesem Fall ist die Bestimmung der Eigenwerte sehr einfach weil die Matrix bereits Dreiecksform hat.
https://www.math.kit.edu/iana3/lehre/hm3etechphys2009w/media/hm3-zsf9.pdf
Was an dem von mir verlinkten Artikel ist unverständlich?
Der letzte Schritt. Ich habe die Eigenvektoren und Eigenwerte. Wäre das Fundamentalsystem dann {(0;1;0)*(e^t), (0;0;1)*(e^4t)}? Muss man grundsätzlich jedes Mal den Eigenvektor zu e^xt multiplizieren, wobei bei x der Eigenwert stehen muss?
Du mußt bei nicht diagonalisierbaren Matrizen den Eigenraum nach und nach erweitern. Das ist das was in 29.3 Fundamentalsysteme für nicht-diagonalisierbare Matrizen steht. Im Heuser ist das Verfahren übrigens ein wenig ... komplizierter erklärt :rofl:. In Walter: Gewöhnliche Differentialgleichungen wird statt dessen die Jordan Normalform heran gezogen. Es ist ein wenig her dass ich das alles gemacht habe, daher ist mir nihct mehr jedes Detail geläufig.
char. Polynom: (z – 1) (z – 4)² = 0
Eig(1) = span((0, 1, 0))
Eig(4) = span((0, 0, 1))
Dann muss das Fundamentalsystem doch so aussehen
{(0, 1, 0) e^t, (0, 0, 1) e^(4 t), (0, 0, 1) t e^(4 t)}
oder nicht?
Aber beim einseten der dritten Lösung kommt man auf
x'(t) = (0, 0, 1) (4 t + 1) e^(4 t)
A x(t) = (0, 0, 1) 4 t e^(4 t)
was ja nicht korrekt ist.
Wie soll man die dritte Lösung berechnen?
Wie gesagt, das ist ein wenig lange her. Prinzipiell wird denke ich schlicht darauf abgezielt, eben die Jordanbasis als Verallgemeinerung der Eigenbasis bei nicht diagonalisierbaren Matrizen zu verwenden. Die entsteht durch Potenzierung der zum Eigenwert lambda gehörigen Matrix A-lambda*I.
Bei Heuser ist die Herleitung wie von mir beschrieben deutlich komplizierter, weil er direkt den Polynomansatz wählt, zeigt das der eben eine Lösung liefert und dann das konkrete Polynom mit Koeffizientenvergleich ermittelt.
Im eindimensional-höhergradigen ist das alles ein wenig einfacher :-).
Die Eigenwerte sind ja {1;4;4}. Die Eigenvektoren zum Eigenwert 1 sind [0;1;0] und zu 4 sind sie [0;0;1]. Wie sieht dann aber das Fundamentalsystem aus?