Anfangswertproblem?
Hallo,
weiß jemand, mit welchem Verfahren man das AWP
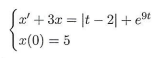
lösen kann und wie?
Ich danke im Voraus für die Beantwortung meiner Frage.
2 Antworten
Die allgemeine Lösung der DGL ist gegeben durch:
x(t) = x(0)*exp(-3t) + int[0, t]{ exp(-3(t - s))*(|s - 2| + exp(9s)) ds}
Verfolge hier den Ansatz über Variation der Konstanten:
dx/dt = ax + u
Wähle als Ansatz: x = xh*c mit homogener Lösung xh und zeitvarianten Konstanten c = c(t). Es folgt durch Einsetzen in die Gleichung:
c*dxh/dt + dc/dt * xh = a*xh*c + u
--> dc/dt * xh = u
--> dc/dt = u/xh
Integration liefert:
c(t) = c(0) + int[0, t]{ u(s)/xh(s) ds}
Somit folgt für den Ansatz:
x = c(0)*xh + int[0, t]{ u(s)*xh(t)/xh(s) ds}
Aus der Bedingung x(0) = x0 folgt
x0 = x(0) = c(0)*xh(0) --> c(0) = x0/xh(0)
Und somit lautet damit die Lösung für die inhomegene DGL
x(t) = x0*xh(t)/xh(0) + int[0, t]{ u(s)*xh(t)/xh(s) ds}
Die inhomogene Lösung xh folgt als Lösung der Gleichung
dx/dt = ax
zu x = exp(at), sodass mit a = -3 damit die beschriebene Gestalt folgt
x(t) = x0*exp(-3t)/1 + int[0, t]{ u(s)*exp(-3t)/exp(-3s) ds}
--> x(t) = exp(-3t) + int[0, t]{ exp(-3(t - s))*u(s) ds}
Substituiere schließlich nur noch u(s) = |s - 2| + exp(9s) und du hast die allgemeine Lösung der DGL gefunden. Es gilt schließlich nur noch das Integral zu bestimmen, wobei hier nur noch die Falluntescheidung zwischen t < 2 und t > 2 getroffen werden muss aufgrund der Betragsfunktion. Das Integral darfst du aber selber berechnen. Hier dann nochmal ein Link der das verallgemeinert:
https://web.mit.edu/2.14/www/Handouts/StateSpaceResponse.pdf
Der Trick ist, dass du eine Fallunterscheidung vornimmst, sodass du den Betrag weglassen kannst.
x'(t) + 3 x(t) = |t – 2| + e^(9 t)
1. Fall: t ≥ 2
x'(t) + 3 x(t) = (t – 2) + e^(9 t)
Ansatz Typ der rechten Seite:
x(t) = a t + b + c e^(9 t)
x'(t) = a + 9 c e^(9 t)
Einsetzen:
a + 9 c e^(9 t) + 3 (a t + b + c e^(9 t)) = t – 2 + e^(9 t)
3 a t + 3 b + a + 12 c e^(9 t) = t – 2 + e^(9 t)
Koeffizientenvergleich:
a = 1/3, b = –7/9, c = 1/12
2. Fall: t < 2
x'(t) + 3 x(t) = –(t – 2) + e^(9 t)
Ansatz Typ der rechten Seite:
x(t) = a t + b + c e^(9 t)
x'(t) = a + 9 c e^(9 t)
Einsetzen:
a + 9 c e^(9 t) + 3 (a t + b + c e^(9 t)) = –(t – 2) + e^(9 t)
3 a t + 3 b + a + 12 c e^(9 t) = –t + 2 + e^(9 t)
Koeffizientenvergleich:
a = –1/3, b = 7/9, c = 1/12.
Insgesamt erhälst du also als eine partikuläre Lösung
x(t) = e^(9 t) / 12 + t / 3 – 7 / 9 für t ≥ 2 und
x(t) = e^(9 t) / 12 – t / 3 + 7 / 9 für t < 2.
Nun noch die homogene Lösung mittels Separation (oder dem Ansatz x(t) = e^(λ t)) berechnen:
x'(t) + 3 x(t) = 0
x'(t) / x(t) = –3
ln|x(t)| = –3 t + K
x(t) = k e^(–3 t)
Allgemeine Lösung:
x(t) = e^(9 t) / 12 + t / 3 – 7 / 9 + k e^(–3 t) für t ≥ 2 und
x(t) = e^(9 t) / 12 – t / 3 + 7 / 9 + k e^(–3 t) für t < 2,
mit beliebigen k. Wegen der Anfangsbedingung x(0) = 5 erhälst du
x(0) = 5
e^(9 • 0) / 12 – 0 / 3 + 7 / 9 + k e^(–3 • 0) = 5
1 / 12 + 7 / 9 + k = 5
k = 149 / 36.
Die Lösung des Anfangswertproblems ist demnach einfach
x(t) = e^(9 t) / 12 + t / 3 – 7 / 9 + 149 / 36 e^(–3 t) für t ≥ 2 und
x(t) = e^(9 t) / 12 – t / 3 + 7 / 9 + 149 / 36 e^(–3 t) für t < 2.
Streng genommen dürfen wir t = 2 nicht mit in den Definitionsbereich aufnehmen, da x'(t) an dieser Stelle unstetig ist,
lim t–>2⁺ x'(t) = x(2) ≈ 49244977,1555534
lim t–>2⁻ x'(t) ≈ 49244976,4888867.