Exponentialfunktion Textaufgabe8?
B und c ? Wie löst man es
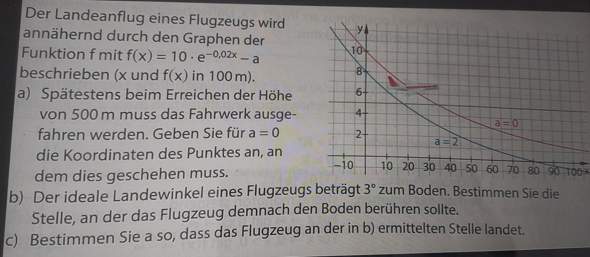
2 Antworten
b)
Wir suchen den x-Wert x*, an der die angelegte Tangente einen Winkel von 3° zur x-Achse hat. Diese Tangentensteigung ergibt sich aus der ersten Ableitung der Funktion f.
Um vom Winkel zur Steigung zu kommen kann man folgendermaßen vorgehen:
Der Tangens eines Winkels alpha in einem rechtwinkligen Dreieck gibt genau das Verhältnis von Gegenkathete zu Ankathete an. Das rechtwinklige Dreieck wird hierbei aus der Tangente (Hypotenuse) und der x-Achse (Ankathete) konstruiert. Werten wir die Funktion f an unserem gesuchten Wert x* aus, dann erhalten wir die Länge der Gegenkathete.
Wir können nun also den vorgegebenen Winkel (im Bogenmaß) einsetzen und dieses Verhältnis (= die Steigung) erhalten:
Diese Steigung wird jetzt mit der ersten Ableitung der Funktion f gleichgesetzt und nach x aufgelöst (mithilfe von ln()).
Wir erhalten x* = 66,963
Jetzt muss die Funktion f so verschoben (um den Wert b) werden, dass sie am Punkt x* gleich 0 ist.
D.h. wir setzen sie zu Null:
0 = f(x*) + b
=> b = - f(x*) = - f(66,963) = -2,62
3/180 *pi ist nur die Umrechnung vom Gradmaß ins Bogenmaß.
Achso stimmt. Ich habe aber ein Problem beim auflösen der gleichung. Als ableitung habe ich etwas negatives raus und sogar im exponenten steht was negatives und kn darf ja nicht negativ sein...
Die Ableitung hat negative Faktoren, das ist richtig so. Die Steigung, die wir mit dem Tangens ausgerechnet haben muss auch "negativ gemacht" werden, denn die Gerade ist ja fallend.
Ein negativer Exponent macht dem ln() nichts aus. Ein negativer Exponent lässt sich auch so schreiben: a^(-1) = 1/abzw. mit allgemeinem Exponent n: a^(-n) = 1/(a^n)
Dieser Ausdruck ist immer größer Null, wenn a > 0 ist. Somit ist es auch ein erlaubter Wert für den Logarithmus Naturalis.
Deine Gleichung müsste nun also so aussehen:
-0,05240778 = -10 * 0,02 * exp(-0,02 * x)
Bei der Division der linken Seite durch die Faktoren auf der rechten Seite fällt das negative Vorzeichen weg. Dann lässt sich auch der ln() anwenden und daraus x bzw. x* berechnen.
Achso....also eigentlich ist ja der tangens 0,05 aber weil die gerade fällt macht man es zu -0,05, habe ich es richtig verstanden?
Genau. Die Tangens-Funktion berechnet das Verhältnis in einem Dreieck. Da kann und sollte dann kein negativer Wert herauskommen. Wenn wir es allerdings im Kontext einer Geradensteigung betrachten, müssen wir das Vorzeichen beachten.
Also was ist dann die Lösung? 66,963 oder 6696,3?
Weil in der aufgabe steht dass x und f(x) in 100m angegeben sind
Wie berechnet man die c? Ich habe die funktion mit dem x Wert gleich 0 gesetz und nach a umgeformt
achso... ja wenn du es in Metern angeben willst, dann sind es 6696,3 m.
Bei der Formulierung "Gib die Stelle an..." würde ich aber behaupten, dass beides möglich und richtig ist.
Ich habe die funktion mit dem x Wert gleich 0 gesetz und nach a umgeformt
genau so, falls du die Funktion f meinst, und nicht die Ableitung f'.
Ob dein a richtig ist, kannst du durch Einsetzen überprüfen.
b)
tan(α) = Gk/Ak = m = f'(x)
daher: α = arctan(m)
also: arctan(f'(x)) = 3 Grad
nach x auflösen
c)
zugehörigen Wert zur Stelle x von Aufgabe b) berechnen und den Punkt in die Funktionsgleichung in Abhängigkeit von a einsetzen, nach a umstellen
Danke. Aber ich verstehe nicht was arctan(f'(x)) ist bzw. Wie ich die steigung bekomme...wo ist denn bei dieser e funktion überhaupt die ankathete und wo die gegenkathete??
Danke. Aber ich verstehe nichtvwarum man für den tangens 3/180 * pi rechnet